Let’s define the settings: we will always consider a measure-preserving system , meaning that
is a probability space and
is a measurable transformation that preserves
:
If , then there exists
such that
. This is easy to see because the family
,
, satisfies a stationary condition
So, if , two of the sets
have positive-measure intersection. In fact, if this is not the case, then
a contradiction. We then get the original Poincaré’s Recurrence Theorem:
Theorem 1 (PRT) If
, then there exists
such that
.
Remark 1 The modern statements of PRT are: if
, then a.e. point
returns to
. This means that
, which obviously implies the above theorem.
This proves more: call a set syndetic if it has bounded gaps, i.e., if there exists
such that
.
Exercise 1 Prove that if
, then the set
is syndetic.
For further discussions about PRT, the reader may consult this paper of Vitaly Bergelson. Altought its simplicity, this is a remarkable result. It implies, for example, that almost every has infinitely many
‘s in its decimal representation, and the same happens for any finite sequence of digits.
As preserves
, it defines a unitary operator
on the Hilbert space
by
, for simplicity denoted from now on as
. With this notation, if
, then
where is the inner product in
, so
such that the sequence ,
, may give more general results than PRT. This is what happens.
Theorem 2 (Von Neumann) If
, then the sequence
,
, converges in
.
This theorem, also known as Mean Ergodic Theorem, is in fact a spectral theoretical result and a more general version holds, given by
Theorem 3 If
is a unitary operator on a Hilbert space
, then the sequence of operators
,
, converges pointwise in norm to the orthogonal projection
onto the subspace of
-fixed elements
.
Proof: When is unitary,
. From the general orthogonal decomposition
we obtain
For , the convergence is obvious. If
, then
By approximation and applying the triangle inequality, the same happens in , which concludes the proof.
Remark 2 Being, as we said, Hilbertian in nature, Theorem 2 also holds when
.
Exercise 2 Under the same conditions of Theorem 3, prove that the same conclusion happens for a sequence
such that
.
Let’s show how to use these convergences to obtain recurrence results.
Proposition 4 Let
be such that
. Then
and
.
Note that satisfies the above conditions.
Proof: Consider the function . Then
and
. Because
minimizes the distance of
to
, we have
. In addition, if we had
, then
, such that
. Integrating, we conclude
a contradiction.
Exercise 3 Using the above proposition, prove that if
, then the set
is syndetic. (Hint: if
, then
converges to
as
.)
So, expressions of the type , from now on called ergodic averages, are important when dealing with recurrence. This will be our main interest in the next posts. For another perspective on Von Neumann’s Theorem and related results, the reader is referred to this Terence Tao’s lecture.
Previous posts: ERT0.
I think in Remark1 you mean to say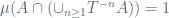 ?
?
By: DB on December 17, 2009
at 4:51 pm
sorry not 1 but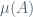 ? [You’re absolutely right! The remark was changed accordingly – M.]
? [You’re absolutely right! The remark was changed accordingly – M.]
By: DB on December 17, 2009
at 4:53 pm