The Willmore conjecture after Fernando Coda Marques and Andre Neves

Posted by: matheuscmss | April 23, 2012

The Willmore conjecture after Fernando Coda Marques and Andre Neves

In the last 5 months I was really happy to see announcements of solutions to important problems and conjectures in several fields of Mathematics. For instance,

(1) Ian Agol announced the proof of the virtual Haken conjecture (see the blog of D. Calegari for three posts on this subject) in ${3}$ -manifold topology,
(2) Fernando Codá Marques and André Neves announced the proof of the Willmore conjecture (see this journal article of F. Morgan for an informal explanation of this 47-years old conjecture),
(3) Alex Eskin, Maxim Kontsevich and Anton Zorich recently completed the proof of a formula for the sum of the Lyapunov exponents of the Kontsevich-Zorich cocycle (announced 15 years ago in this paper of M. Kontsevich), and
(4) Alex Eskin and Maryam Mirzakhani recently announced the proof of a Ratner type theorem (classification of invariant measures) in the (non-homogenous) setting of the moduli spaces of Abelian differentials.

In particular, since I’ve already met Fernando Codá Marques, André Neves, Anton Zorich and Alex Eskin before in several occasions, I would like to take the opportunity (and liberty) to congratulate them for these quite impressive works! (indeed, besides presenting excellent results, the articles in the second, third and fourth items above have 95, 106 and 152 pages resp. 🙂 )

My current plan is to dedicate some posts in this blog to expose a few points of the articles mentioned in the three last items above. More concretely, the rest of today’s post is entirely dedicated to the presentation of the solution of the Willmore conjecture by Fernando and André (here I’ll call them by their first names as I think they will not mind 🙂 ). Then, in (a?) future post(s?), I will discuss the article of Alex, Anton and M. Kontsevich on the sum of Lyapunov exponents of the Kontsevich-Zorich cocycle. Finally, I will complete this “series” with some post(s?) about the Ratner type theorem of Alex and M. Mirzakhani based on some notes I took from the course Alex gave in Luminy/Marseille a few weeks ago.

Before proceeding further, let me make some disclaimers and comments. Firstly, the task of writing today’s post was substantially simplified by the fact that Fernando and André wrote an excellent outline of their arguments and ideas in Section 2 of their article. In particular, today I’ll essentially follow their outline, but please beware that maybe I introduced some mistakes in this process (and, of course, such mistakes are my responsibility only). Secondly, the article of item (3) will be the subject of a talk by Pascal Hubert at Séminaire Bourbaki in October 2012. In particular, he will prepare a serious set of notes for his talk, so that my posts around this topic should be seen as an informal preparation to Pascal’s notes. Finally, concerning the article in item (4) above, Alex Eskin made available in his webpage (see here) an excellent set of notes around his minicourse: indeed, the set of notes by Alex are so pleasant to read that I’ve immediately changed my initial plan of posting my original notes here and I’ll content myself to make a few comments around the techniques used by Alex and M. Mirzakhani, e.g., I’ll try to post my notes from the minicourse (also in Luminy/Marseille) taught by J.-F. Quint around the so-called “exponential drift” idea (from his celebrated paper with Y. Benoist).

After these comments, let’s start (below the fold) the discussion of the Willmore conjecture and its solution by Fernando and André!

1. Introduction

Let ${\widetilde{\Sigma}\hookrightarrow\mathbb{R}^3}$ be a closed (i.e., compact and boundaryless) immersed surface of ${\mathbb{R}^3}$ . Among the most simple geometric invariants one can associate to ${\widetilde{\Sigma}}$ , we arguably have the Gaussian curvature ${\widetilde{K}=\widetilde{K}(p)}$ and the mean curvature ${\widetilde{H}=\widetilde{H}(p)}$ (at each point ${p\in\widetilde{\Sigma}}$ ) obtained from the determinant and the trace of the so-called second fundamental form ${\widetilde{A}=\widetilde{A}(p):T_p\widetilde{\Sigma}\rightarrow T_p\widetilde{\Sigma}}$ (a ${2\times2}$ linear operator/matrix whose eigenvalues are the principal curvatures of ${\widetilde{\Sigma}}$ at ${p}$ ). For a excellent exposition of these concepts see, e.g., M. do Carmo’s classical book “Differential geometry of curves and surfaces”.

In this language, the Willmore energy ${\widetilde{\mathcal{W}}(\widetilde{\Sigma})}$ is

$\displaystyle \widetilde{\mathcal{W}}(\widetilde{\Sigma}) = \int_{\widetilde{\Sigma}} \widetilde{H}^2\,d\widetilde{\Sigma}$

where ${d\widetilde{\Sigma}}$ is the natural area form of ${\widetilde{\Sigma}}$ .

The Willmore energy naturally appears in some physical (study of elastic shells) and biological (study of cell membranes) contexts, where it is sometimes called bending energy.

In the mathematical context, it was known to be invariant under conformal transformations of ${\mathbb{R}^3}$ by e.g. W. Blaschke, and a very natural geometric (variational) problem consists in its minimization within a given class of immersed closed surfaces ${\widetilde{\Sigma}\hookrightarrow\mathbb{R}^{3}}$ .

Here, it is possible to show that for any immersed closed surface ${\widetilde{\Sigma}\hookrightarrow\mathbb{R}^3}$

$\displaystyle \widetilde{\mathcal{W}}(\widetilde{\Sigma})\geq 4\pi = \widetilde{\mathcal{W}}(S^2(r))$

where ${S^2(r)\subset\mathbb{R}^3}$ is the } of radius ${r>0}$ . Moreover, ${\widetilde{\mathcal{W}}(\widetilde{\Sigma})= 4\pi}$ if and only if ${\widetilde{\Sigma}}$ is a round sphere. In other words, the round spheres of ${\mathbb{R}^3}$ minimize the Willmore energy in the class of all closed immersed surfaces. Actually, the proof of this fact is not hard:

Denoting the principal curvatures by ${k_1\geq k_2}$ , and recalling that the mean curvature is ${\widetilde{H}=(k_1+k_2)/2}$ , and the Gaussian curvature is ${\widetilde{K}=k_1k_2}$ , we get from the abstract equality ${(k_1+k_2)^2=(k_1-k_2)^2+4k_1k_2}$ that
$\displaystyle \widetilde{\mathcal{W}}(\widetilde{\Sigma})=\int_{\widetilde{\Sigma}} \widetilde{H}^2\,d\widetilde{\Sigma} = \frac{1}{4}\int_{\widetilde{\Sigma}} (k_1-k_2)^2\,d\widetilde{\Sigma}+\int_{\widetilde{\Sigma}} \widetilde{K}\,d\widetilde{\Sigma}\geq \int_{\widetilde{\Sigma}} \widetilde{K}\,d\widetilde{\Sigma}$

On the other hand, by the Gauss-Bonnet theorem, ${\int_{\widetilde{\Sigma}} \widetilde{K}\,d\widetilde{\Sigma}=2\pi\chi(\widetilde{\Sigma})}$ . Therefore, assuming that ${\widetilde{\Sigma}}$ is topologically a sphere, i.e., it has genus ${g=0}$ and Euler characteristic ${\chi(\widetilde{\Sigma})=2-2g=2}$ , we can conclude that

$\displaystyle \widetilde{\mathcal{W}}(\widetilde{\Sigma})\geq \int_{\widetilde{\Sigma}} \widetilde{K}\,d\widetilde{\Sigma}=4\pi$

and the equality holds if and only if

$\displaystyle \frac{1}{4}\int_{\widetilde{\Sigma}} (k_1-k_2)^2\,d\widetilde{\Sigma}=0$

that is, ${k_1=k_2}$ at all points of ${\widetilde{\Sigma}}$ , i.e., all points are umbilical, and this last property allows to show ${\widetilde{\mathcal{W}}(\widetilde{\Sigma})=4\pi}$ precisely when ${\widetilde{\Sigma}}$ is a round sphere.
In general (i.e., when ${\widetilde{\Sigma}}$ has higher genus ${g\geq 1}$ ), the calculation above is not useful because ${\int_{\widetilde{\Sigma}} \widetilde{K}\,d\widetilde{\Sigma}=2\pi\chi(\widetilde{\Sigma})=2\pi(2-2g)\leq 0}$ , that is, the estimate ${\widetilde{\mathcal{W}}(\widetilde{\Sigma})\geq \int_{\widetilde{\Sigma}} \widetilde{K}\,d\widetilde{\Sigma}}$ relying on Gauss-Bonnet theorem is weaker than the trivial bound ${\widetilde{\mathcal{W}}(\widetilde{\Sigma})= \int_{\widetilde{\Sigma}} H^2\,d\widetilde{\Sigma}\geq0}$ . However, one can overcome this by using the Chern-Lashof inequality
$\displaystyle \int_{\widetilde{\Sigma}} |\widetilde{K}|\,d\widetilde{\Sigma}\geq 2\pi(2+2g)$

In fact, denoting by ${a:=\int_{\{\widetilde{K}>0\}} \widetilde{K}\,d\widetilde{\Sigma}}$ and ${b:=\int_{\{\widetilde{K}\leq0\}} \widetilde{K}\,d\widetilde{\Sigma}}$ , we have

$\displaystyle a+b=\int_{\widetilde{\Sigma}} \widetilde{K}\,d\widetilde{\Sigma}=(2-2g)2\pi$

and

$\displaystyle a-b=\int_{\widetilde{\Sigma}} |\widetilde{K}|\,d\widetilde{\Sigma}\geq 2\pi(2+2g)$

so that ${a\geq 4\pi}$ . Now, we can use ${(k_1+k_2)^2=(k_1-k_2)^2+4k_1k_2}$ to the region ${\{\widetilde{K}>0\}}$ to get that

$\displaystyle 4\pi\leq a\leq \int_{\{\widetilde{K}>0\}} \widetilde{K}\,d\widetilde{\Sigma} + \frac{1}{4}\int_{\{\widetilde{K}>0\}} (k_1-k_2)^2\,d\widetilde{\Sigma}\leq \widetilde{\mathcal{W}}(\widetilde{\Sigma})$

In any event, once one realizes that the minimization of the Willmore energy in the class of all immersed compact surfaces of ${\mathbb{R}^3}$ is not difficult, one can follow T. Willmore and ask about the problem of minimizing the Willmore energy in the class of immersed torii of ${\mathbb{R}^3}$ :

Willmore conjecture (1965). ${\widetilde{W}(\widetilde{\Sigma})\geq 2\pi^2(>4\pi)}$ for any imersed torus ${\widetilde{\Sigma}\hookrightarrow\mathbb{R}^3}$ .

The equality ${\widetilde{W}(\widetilde{\Sigma}_c)=2\pi^2}$ is attained by the torus of revolution ${\widetilde{\Sigma}_c}$ obtained by rotating a circle of radius ${1}$ with center at distance ${\sqrt{2}}$ from the axis of revolution:

$\displaystyle (u,v)\mapsto ((\sqrt{2}+\cos u)\cos v, (\sqrt{2}+\cos u) \sin v, \sin u)\in\mathbb{R}^3$

See, e.g., P. Nylander’s post here for nice pictures of this torus.

This torus of revolution ${\widetilde{\Sigma}_c}$ is the stereographical projection ${\pi:S^3-\{(0,0,0,1)\}\rightarrow\mathbb{R}^3}$ of the Clifford torus ${\Sigma_c=S^1(1/\sqrt{2})\times S^1(1/\sqrt{2})\subset S^3}$ , i.e., ${\widetilde{\Sigma}_c=\pi(\Sigma_c)}$ .

More generally, the Willmore conjecture can be seen as a question about immersed closed surfaces on ${S^3}$ by means of the stereographical projection ${\pi}$ : indeed, given ${\Sigma\subset S^3}$ , by putting ${\widetilde{\Sigma}=\pi(\Sigma)}$ , one has that

$\displaystyle \widetilde{W}(\widetilde{\Sigma}) = \int_{\widetilde{\Sigma}} \widetilde{H}^2\,d\widetilde{\Sigma} = \int_{\Sigma}(1+H^2)\,d\Sigma:=\mathcal{W}(\Sigma)$

where ${H}$ is the mean curvature of ${\Sigma\subset S^3}$ . So, the minimization of ${\mathcal{W}(\widetilde{\Sigma})}$ is equivalent to the minimization of ${\mathcal{W}(\Sigma)}$ . For this reason, we will also call ${\mathcal{W}(\Sigma)}$ the Willmore energy of ${\Sigma\subset S^3}$ .

Even though this reformulation is not sophisticated, it is very interesting given that the Willmore conjecture is a variational (minimization) problem. For instance, if one consider a sequence of surfaces ${M_i}$ converging to the infimum of the Willmore energy, and one try to construct a surface ${M}$ minimizing the Willmore energy by taking some “limit” along a subsequence of ${M_i}$ , it is better to know that ${M_i\subset S^3}$ than ${M_i\subset\mathbb{R}^3}$ because ${S^3}$ is compact but ${\mathbb{R}^3}$ is not.

Concerning some previously known results towards Willmore conjecture, one has:

(a) it was shown by P. Li and S.-T. Yau that if an immersion ${f:\Sigma\rightarrow S^3}$ covers a points ${x\in S^3}$ at least ${k\geq 1}$ times, then ${\mathcal{W}(\Sigma)\geq 4\pi k}$ . In particular, if ${\Sigma}$ is an immersed non-embedded surface (i.e., ${k>1}$ at some ${x\in S^3}$ ), then ${\mathcal{W}(\Sigma)\geq 8\pi>2\pi^2}$ . In other words, it suffices to estimate ${\mathcal{W}(\Sigma)}$ for embedded ${\Sigma\hookrightarrow S^3}$ ;
(b) L. Simon proved the existence of a torus minimizing the Willmore energy (and later this result was generalized by M. Bauer and E. Kuwert for higher genus cases);
(c) critical points ${\Sigma}$ of the Willmore functional ${\mathcal{W}}$ are called Willmore surfaces and the Euler-Lagrangeequation of this functional is
$\displaystyle \Delta H + 2(H^2-K)H=0$

where ${\Delta}$ is the Laplacian on ${\Sigma}$ and ${K}$ is the Gaussian curvature of ${\Sigma}$ . From this equation (sometimes called Willmore equation), we see that minimal, i.e., ${H\equiv 0}$ , surfaces of ${S^3}$ (such as the ones constructed by B. Lawson in this paper here) are Willmore surfaces, but they are not the sole ones (see, e.g., the articles of R. Bryant, U. Pinkall). For more information on the analytical aspects of the Willmore equation, see, e.g., this article of T. Rivière.

In a recent breakthrough article, Fernando Codá Marques and André Neves proved the following theorem:

Theorem 1 (F. C. Marques and A. Neves) Let ${\Sigma\hookrightarrow S^3}$ be an embedded closed surface of genus ${g\geq 1}$ . Then,

$\displaystyle \mathcal{W}(\Sigma)\geq 2\pi^2.$

Moreover, ${\mathcal{W}(\Sigma)=2\pi^2}$ if and only if ${\Sigma}$ is conformal to the Clifford torus ${\Sigma_c}$ .

By item (a) above, this profound result implies the Willmore conjecture.

For the proof of Theorem 1, Fernando and André firstly reduce the case of a general ${\Sigma}$ to the case of a minimal ${\Sigma}$ with the aid of a theorem min-max theorem (see Theorem 2 below).

Remark 1 Here, in ${0}$ th order of approximation, the “philosophy” behind this reduction is the fact that the Willmore energy

$\displaystyle \mathcal{W}(\Sigma)=\int_{\Sigma}(1+H^2)\,d\Sigma = \int_{\Sigma}1 \,d\Sigma=\textrm{area}(\Sigma)$

coincides with the area functional when ${\Sigma}$ is minimal (i.e., ${H\equiv 0}$ ), and the problem of studying the area of minimal surfaces is a classical subject in Differential Geometry.

Roughly speaking, given a general embedded closed surface ${\Sigma\subset S^3}$ of genus ${g\geq 1}$ , they consider its natural “min-max homotopy class” ${\Pi}$ and the corresponding width ${L(\Pi)}$ . Informally, we can describe general homotopy classes and their widths in the case of ${2}$ -dimensional surfaces inside a compact ${3}$ -dimensional manifold ${M^3}$ as follows.

Given ${n\geq 1}$ , let ${I^n=[0,1]^n}$ be the unit cube of ${\mathbb{R}^n}$ and let ${\Phi}$ be a (continuous) map defined on ${I^n}$ such that ${\Phi(x)}$ is a compact boundaryless surface of ${M^3}$ for each ${x\in I^n}$ . We say that two such maps ${\Phi_0}$ and ${\Phi_1}$ are homotopic (relatively to ${\partial I^n}$ ) if we can find a (continuous) map ${\Psi}$ defined on ${I^{n+1}=I\times I^n}$ such that

${\Psi(y)}$ is a compact boundaryless surface of ${M^3}$ for all ${y=(t,x)\in I^{n+1}=I\times I^n}$ ;
${\Psi(0,x)=\Phi_0(x)}$ and ${\Psi(1,x)=\Phi_1(x)}$ for all ${x\in I^n}$ ;
${\Psi(t,x)=\Phi_0(x)=\Phi_1(x)}$ for all ${t\in I}$ , ${x\in\partial I^n}$ .

Below we illustrate the concept of homotopy with two pictures in a low-dimensional setting, that is, $M=S^2$ (instead of a $3$ -dimensional manifold) and the maps $\Phi$ take values in the space of curves (instead of surfaces). For the first picture, we took $n=0$ , so that $I^0=\{0\}$ and we drew the images of $I^0$ under $\Phi_0$ and $\Phi_1$ by the blue and red curves resp., while for the second picture we took $n=1$ , so that $I^1=I$ , the images of $\Phi_0$ , resp. $\Phi_1$ , is the family of blue, resp. red, curves, and the image of the boundary $\partial I$ are the two trivial (degenerate) “curves” corresponding to the north and south poles of $S^2$ .

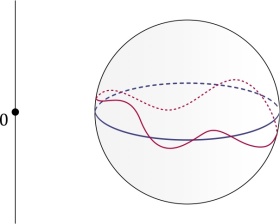
The homotopy class ${\Pi}$ of ${\Phi_0}$ is the set of all ${\Phi_1}$ homotopic to ${\Phi_0}$ , and the width ${L(\Pi)}$ of ${\Pi}$ is

$\displaystyle L(\Pi) = \inf\limits_{\Phi_1\in\Pi}\sup\limits_{x\in I^n} \textrm{area}(\Phi_1(x))$

Remark 2 The formal definition of homotopy classes (and their widths) in the article of Fernando and André rely on some concepts from Geometric Measure Theory such as (integral) currents, varifolds, and flat metric and the flat topology (based on the notion of mass) in the space of integral currents. In particular, the maps ${\Phi}$ above associate an integral current without boundary ${\Phi(x)}$ to each ${x\in I^n}$ , and ${\Phi}$ is assumed to be continuous in the flat topology. Similarly, the homotopy ${\Psi}$ is continuous in the mass topology. See Sections 4 and 7 of the article of Fernando and André for more details.

Example 1 For the homotopy class ${\Pi_0}$ of ${\Phi_{(0)}(s):=\{x_4=2s-1\}\subset S^3}$ (roughly corresponding to the family of blue circles in the second picture above) for ${s\in I=[0,1]}$ , it is possible to show (the intuitive fact) that ${L(\Pi_0)=4\pi}$ .

Remark 3 In some sense, the homotopy class ${\Pi_0}$ of the previous example can be though as an element of the “homotopy group” ${\pi_1(\mathcal{S},0)}$ where ${\mathcal{S}}$ is the space of surfaces in ${S^3}$ and ${0}$ is the trivial surface (of area zero).

In the case of a closed embedded surface ${\Sigma}$ of ${S^3}$ of genus ${g\geq 1}$ , Fernando and André associate a certain ${5}$ -dimensional min-max homotopy class ${\Pi}$ (i.e., they consider the homotopy class of a certain ${\Phi}$ related to ${\Sigma}$ and defined on ${I^5}$ ) and they show the following min-max result:

Theorem 2 (F. C. Marques and A. Neves) Let ${\Sigma\subset S^3}$ be a closed embedded surface of genus ${g\geq 1}$ . Then, there exists a minimal embedded surface ${\widehat{\Sigma}\subset S^3}$ of genus ${g\geq 1}$ (maybe not connected and possibly with multiplicities) such that

$\displaystyle 4\pi<\textrm{area}(\widehat{\Sigma})=L(\Pi)\leq\mathcal{W}(\Sigma)$

where ${\Pi}$ is the min-max homotopy class of ${\Sigma}$ .

As we already mentioned, this permits to reduce the proof of Theorem 1 for a general ${\Sigma\subset S^3}$ to the study of the area of a minimal ${\widehat{\Sigma}\subset S^3}$ . Here, Fernando and André show that:

Theorem 3 (F. C. Marques and A. Neves) Let ${\widehat{\Sigma}\subset S^3}$ be a embedded closed minimal surface of genus ${g\geq 1}$ . Then,

$\displaystyle \textrm{area}(\widehat{\Sigma})\geq 2\pi^2.$

Moreover, the equality ${\textrm{area}(\widehat{\Sigma})=2\pi^2}$ holds if and only if ${\widehat{\Sigma}}$ is isometric to the Clifford torus ${\Sigma_c}$ .

Of course, by combining Theorems 2 and 3, the inequality ${\mathcal{W}(\Sigma)\geq 2\pi^2}$ in the statement of Theorem 1 “essentially” follows. Indeed, we said “essentially” because if the minimal surface ${\widehat{\Sigma}}$ of genus ${g\geq 1}$ were known to be connected and of multiplicity ${1}$ , then Theorem 1 would really follow. Of course, this is not true in general, but, as we’ll see by the end of this post, it is easy to conclude Theorem 1 from Theorems 2 and 3. Also, the fact that ${\mathcal{W}(\Sigma)=2\pi^2}$ characterizes the conformal class of the Clifford torus ${\Sigma_c}$ is not a direct consequence of Theorems 2 and 3 as stated above, but nevertheless we’ll see that it follows from the arguments used in the proofs of these results anyway.

In any event, after these highlights of the main results obtained by Fernando and André, we pass to the description (compare with Section 2 of the article of Fernando and André) of the general strategy of the proofs of Theorems 1, 2 and 3.

2. Strategy of the proof of Theorem 2

A large portion of the article of Fernando and André is devoted to the careful construction of a min-max theory à la Almgren-Pitts in order to realize the width of certain homotopy classes by the area of minimal surfaces. In the next subsection, a prototypical result of this min-max theory is stated.

2.1. Prototype of min-max theorem

Let ${M=M^3}$ be a compact ${3}$ -dimensional manifold and let ${\Pi}$ be a homotopy class of a (continuous) map ${\Phi}$ associating a compact surface of ${M}$ to each ${x\in I^n=[0,1]^n}$ .

Theorem 4 (Min-max theorem) Suppose that

$\displaystyle L(\Pi)>\sup\limits_{x\in\partial I^n}\textrm{area}(\Phi(x)).$

Then, there exists ${\Sigma\subset M}$ a smooth embedded minimal surface (maybe not connected and with multiplicities) such that

$\displaystyle \textrm{area}(\Sigma)=L(\Pi).$

Furthermore, given ${\{\Phi_i\}_{i\in\mathbb{N}}\subset\Pi}$ with

$\displaystyle \lim\limits_{i\rightarrow\infty} \sup\limits_{x\in I^n} \textrm{area}(\Phi_i(x)) = L(\Pi),$

we can select ${x_i\in I^n}$ , ${i\in\mathbb{N}}$ , with

$\displaystyle \Sigma=\lim\limits_{i\rightarrow\infty}\Phi_i(x_i).$

In rough terms, the condition ${L(\Pi)>\sup\limits_{x\in\partial I^n}\textrm{area}(\Phi(x))}$ in the previous theorem is setup as a sort of barrier at the boundary. In this language, the min-max theorem above says that the variational problem of realizing the width ${L(\Pi)}$ of a homotopy class ${\Pi}$ by the area of a minimal surface can be solved by taking the limit of an appropriate sequence ${\Phi_i(x_i)}$ of surfaces whose areas approximates ${L(\Pi)}$ because the “barrier condition” prohibits ${\Phi_i(x_i)}$ to “escape” through the boundary (and so ${\Phi_i(x_i)}$ must converge).

Of course, the statement above is an approximation of the min-max theorem proved by Fernando and André. For a more precise result, see Theorem 8.5 (and also Proposition 8.4) in their article. As we already mentioned, the proof of the min-max theorem (or, more precisely, the proof of Proposition 8.4) is quite long and technical and it occupies a significant portion of the article (namely, Sections 13, 14, 15 and Appendix C). In particular, a detailed discussion of this part of the article is out of the scope of this post, and we will take this result for granted in what follows.

Remark 4 As it is mentioned by Fernando and André in the article, by analogy with Morse theory, the minimal surface ${\Sigma}$ in the min-max theorem above is expected to have index ${\leq n}$ (because it comes from a ${n}$ -parameter family of surfaces). In general, this seems a delicate issue to verify, but, nevertheless, we will see (during the proof of Theorem 3) that this is the case for the min-max homotopy class of the Clifford torus (where ${n=5}$ ).

Once we dispose of the min-max theorem, we continue the outline of the proof of Theorem 2 by sketching (in the next three subsections) the construction of the min-max homotopy class associated to a smooth compact embedded surface ${\Sigma\subset S^3}$ .

2.2. Canonical family

Let ${B^4=\{x\in\mathbb{R}^4: |x|<1\}}$ be the open unit ball of ${\mathbb{R}^4}$ . For each ${v\in B^4}$ , let ${F_v:S^3\rightarrow S^3}$ be the conformal map

$\displaystyle F_v(x):=\frac{(1-|v|^2)}{|x-v|^2}(x-v) -x$

Given ${\Sigma\subset S^3}$ smooth compact embedded surface, we have the following canonical family of surfaces

$\displaystyle \Sigma_{(v,t)}:=\partial\{x\in S^3: d_v(x)<t\}, \quad (v,t)\in B^4\times [-\pi,\pi].$

Here, ${d_v(x)}$ is the oriented distance between ${x}$ and the surface ${F_v(\Sigma)}$ in the canonical (round) metric ${d}$ of ${S^3}$ , that is, by choosing an orientation of ${\Sigma}$ , we can write ${S^3-\Sigma=A^{int}\cup A^{ext}}$ where ${A^{int}}$ is the “interior” of ${\Sigma}$ (a connected component of ${S^3-\Sigma}$ ) and ${A^{ext}}$ is the “exterior” of ${\Sigma}$ (the other connected component of ${S^3-\Sigma}$ ), and we put

$\displaystyle d_v(x) = \left\{\begin{array}{cl}d(x,F_v(\Sigma)) & \textrm{if } x\in F_v(A^{ext}) \\ -d(x,F_v(\Sigma)) & \textrm{if } x\in F_v(A^{int})\end{array}\right.$

Remark 5 Since the diameter of ${S^3}$ is ${\pi}$ , we have that ${\Sigma_{v,-\pi}}$ and ${\Sigma_{v,\pi}}$ are trivial (zero area) surfaces for all ${v\in B^4}$ .

Because ${F_v}$ is conformal, we have that ${\mathcal{W}(F_v(\Sigma))=\mathcal{W}(\Sigma)}$ for every ${v\in B^4}$ . On the other hand, as it was shown by A. Ros, one has

$\displaystyle \textrm{area}(\Sigma_{(v,t)})\leq\mathcal{W}(\Sigma) - \frac{\sin^2t}{2}\int_{\Sigma} |\mathring{A}|^2 d\Sigma\leq\mathcal{W}(\Sigma)$

where ${\mathring{A}}$ is the traceless part of the second fundamental form ${A}$ of ${\Sigma}$ . In fact, the proof of this estimate is not difficult: it is a direct (one-page) computation with ${F_v}$ that can be found in page 15 (cf. Theorem 3.4) of the article of Fernando and André.

In resume, given ${\Sigma\subset S^3}$ smooth compact embedded surface, we have a canonical ${5}$ -dimensional family of surfaces ${\Sigma_{(v,t)}}$ , ${(v,t)\in B^4\times[-\pi,\pi]}$ such that

$\displaystyle \textrm{area}(\Sigma_{(v,t)})\leq \mathcal{W}(\Sigma)=\mathcal{W}(F_v(\Sigma)) \ \ \ \ \ (1)$

In view of this estimate and the statement of Theorem 2, it is tempting to try to apply the Min-Max Theorem 4 to the canonical family ${\Sigma_{(v,t)}}$ , ${(v,t)\in B^4\times[-\pi,\pi]}$ . However, this doesn’t quite work: ${B^4}$ is not compact, and any attempt to “reasonably” extend the canonical family to ${\overline{B}^4\times [-\pi,\pi]\simeq I^5}$ is not continuous, e.g., in the flat topology (see Remark 2), so that such extended canonical families don’t define reasonable homotopy classes. For instance, while ${F_v(\Sigma)}$ and ${\Sigma_{(v,t)}}$ still make sense for ${B^4\ni v\rightarrow p\in S^3-\Sigma=\partial B^4-\Sigma}$ , e.g., ${\Sigma_{(v,t)}\rightarrow\partial B_{\pi+t}(p)}$ or ${\partial B_t(-p)}$ as ${v\rightarrow p\in S^3-\Sigma=A^{int}\cup A^{ext}}$ depending on whether ${p\in A^{ext}}$ or ${A^{int}}$ , the same is not true for ${B^4\ni v\rightarrow p\in\Sigma}$ in the sense that the limit of ${\Sigma_{(v,t)}}$ as ${v\rightarrow p\in\Sigma}$ depend on the “angle of convergence”: more precisely, denoting by ${N(p)}$ the unit normal vector to ${\Sigma\subset S^3}$ at ${p}$ , if

$\displaystyle v_n=|v_n|(\cos(s_n)p+\sin(s_n)N(p))$

approaches ${p\in \Sigma}$ (i.e., ${|v_n|<1}$ , ${|v_n|\rightarrow 1}$ and ${s_n\rightarrow 0}$ as ${n\rightarrow\infty}$ ), then

$\displaystyle \Sigma_{(v_n,t)}\rightarrow \partial B_{\frac{\pi}{2}-\theta+t}(-\sin(\theta)p-\cos(\theta)N(p))$

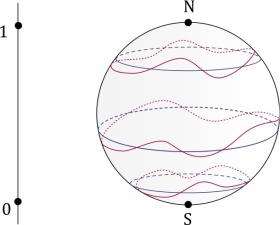
where ${\theta=\lim\limits_{n\rightarrow\infty}\arctan s_n/(1-|v_n|)\in [-\pi/2,\pi/2]}$ . See the picture below for an illustration (in low-dimensions) of a sequence ${v_n}$ approaching a point ${p}$ in a totally geodesic sphere (equator) ${\Sigma}$ .

A detailed discussion of these facts about the behavior of ${\Sigma_{(v,t)}}$ as ${v\rightarrow S^3=\partial B^4}$ is performed in Section 5 of the article of Fernando and André (see Proposition 5.3, Lemma 5.4 and Appendix B).

In any case, we just saw that the main obstacle to “reasonably” extend the canonical family ${\Sigma_{(v,t)}}$ to ${\overline{B^4}\times [-\pi,\pi]}$ is the set ${\Sigma}$ . Here, Fernando and André propose to overcome this difficulty by “blowing up” ${\Sigma}$ , the topic of our next subsection.

2.3. A blow-up procedure

Fix ${\varepsilon>0}$ small and let ${\Omega_{\varepsilon}}$ be the tubular neighborhood of ${\Sigma}$ of radius ${\varepsilon>0}$ in ${\overline{B^4}}$ , i.e.,

$\displaystyle \Omega_{\varepsilon}=\left\{\Lambda(p,s_1,s_2):=(1-s_1)(\cos(s_2)p+\sin(s_2)N(p)); \right.$

$\displaystyle \left. |(s_1,s_2)|:=\sqrt{s_1^2+s_2^2}<\varepsilon, s_1\geq 0\right\}$

Then, one considers a continuous map ${T:\overline{B^4}\rightarrow\overline{B^4}}$ such that:

${T}$ is a homeomorphism between ${B^4-\overline{\Omega_{\varepsilon}}}$ to ${B^4}$ , and
${T}$ sends ${\overline{\Omega_{\varepsilon}}}$ to ${\Sigma}$ by projection to the nearest point.

More concretely, one can define ${T}$ to be the identity map on ${\overline{B^4}-\Omega_{3\varepsilon}}$ and ${T(\Lambda(p,s_1,s_2)) = \Lambda(p,\phi(|(s_1,s_2)|)s_1,\phi(|(s_1,s_2)|)s_2)}$ where ${\phi}$ is a smooth bump function, ${\phi}$ equals to ${0}$ on ${[0,\varepsilon]}$ , ${\phi}$ is strictly increasing on ${[\varepsilon,2\varepsilon]}$ , and ${\phi}$ equals to ${1}$ on ${[2\varepsilon,3\varepsilon]}$ .

Below we give a pictorial description of ${B^4-\overline{\Omega_{\varepsilon}}}$ when ${\Sigma}$ is a meridian (totally geodesic sphere), where the reader can (hopefully) visualize what is the role of the blow-up map ${T}$ .

Using ${T}$ , Fernando and André modify the initial canonical family ${\Sigma_{(v,t)}}$ by introducing the family ${C(v,t)=\Sigma_{(T(v),t)}}$ for ${(v,t)\in (B^4-\overline{\Omega_{\varepsilon}})\times [-\pi,\pi]}$ . Here, since we removed a tubular neighborhood ${\Omega_{\varepsilon}}$ of ${\Sigma}$ , one sees from the features of ${T}$ that the problem of dependence on the “angle of convergence” for ${\Sigma_{(v,t)}}$ is now solved for ${C(v,t)}$ : morally, the selection of ${\Omega_{\varepsilon}}$ and the definition of ${T}$ serves to stop before reaching ${\Sigma}$ and to choose a “definite angle of convergence”.

In particular, it is not hard to convince oneself that the new family ${C}$ admits a “reasonable” — continuous in the flat topology on the space of integral currents without boundary, see Remark 2 — extension to ${\overline{B^4-\Omega_{\varepsilon}}\times [-\pi,\pi]}$ . Then, one can further extend ${C}$ to ${\Omega_{\varepsilon}}$ so that ${C}$ is constant in the radial direction, i.e., ${C(\Lambda(p,s_1,s_2)):=C(\Lambda(p,\varepsilon,s_2))}$ .

In this way, Fernando and André show (see Theorem 5.1 of their article) that one gets a “reasonable” family ${C}$ defined on ${\overline{B^4}\times[-\pi,\pi]}$ such that

${\textrm{area}(C(v,-\pi))=\textrm{area}(C(v,\pi))=0}$ for all ${v\in\overline{B^4}}$ ;
${C(v,t)}$ is a geodesic sphere of ${S^3}$ when ${v\in S^3\cup\overline{\Omega_{\varepsilon}}}$ ;
for each ${v\in S^3}$ , there exists an unique ${s(v)\in[-\pi/2,\pi/2]}$ such that ${C(v,s(v))}$ is a totally geodesic sphere of ${S^3}$ , i.e.,
$\displaystyle C(v,s(v))=\partial B_{\pi/2}(\overline{Q}(v))$

for some ${\overline{Q}(v)\in S^3}$ ; for example, if ${v\in S^3-\Omega_{3\varepsilon}}$ , then ${\overline{Q}(v)=\pm v}$ and ${s(v)=\pm\pi/2}$ depending on whether ${v}$ belongs to the interior ${A^{int}}$ or the exterior ${A^{ext}}$ of ${\Sigma}$ .

Actually, in the last item, ${\overline{Q}(v)}$ can take two values in principle, but, by considering oriented surfaces, one has ${\partial B_{\pi/2}(p)\neq \partial B_{\pi/2}(-p)}$ , and thus ${\overline{Q}(v)}$ is also unique (as well as ${s(v)}$ ).

In particular, by the second and third items above, we have that

$\displaystyle \sup\limits_{(v,t)\in\partial(\overline{B^4}\times[-\pi,\pi])}\textrm{area}(C(v,t))=4\pi \ \ \ \ \ (2)$

Later on, we’ll see that this equality is a “barrier at boundary” condition in the sense discussed in Subsection 2, but, for now we’ll use the family ${C(v,t)}$ to complete the definition of the min-max family associated to ${\Sigma\subset S^3}$ in the next subsection.

2.4. Min-max family associated to ${\Sigma\subset S^3}$

Choose ${f:I^4\rightarrow \overline{B^4}}$ a homeomorphism (so that ${f}$ is a homeomorphism between ${\partial I^4}$ and ${S^3}$ ) and ${\widehat{s}:\overline{B^4}\rightarrow[-\pi/2,\pi/2]}$ an extension of ${s:S^3\rightarrow [-\pi/2,\pi/2]}$ (for a concrete choice of ${\widehat{s}}$ , see Section 6 of the article of Fernando and André). Using ${f}$ and ${\widehat{s}}$ , we define the min-max family ${\Phi}$ associated to ${\Sigma}$ by the following reparametrization of ${C}$ :

$\displaystyle \Phi(x):=\Phi(\widetilde{x},t):=C(f(\widetilde{x}), 2\pi(2t-1)+\widehat{s}(f(\widetilde{x})), \quad x=(\widetilde{x},t)\in I^5=I^4\times I$

From the definitions, we have that the min-max family ${\Phi}$ verify the following properties (see Theorem 6.3 of the article of Fernando and André):

(a) for each ${\widetilde{x}\in\partial I^4}$ , ${\Phi(\widetilde{x},t)}$ is a totally geodesic sphere if and only if ${t=1/2}$ ;
(b) by Equation (1)(A. Ros’ estimate) above, one has
$\displaystyle \sup\limits_{x\in I^5}\textrm{area}(\Phi(x))\leq\mathcal{W}(\Sigma)$
(c) by Equation (2)(“barrier at the boundary” condition), one has
$\displaystyle \sup\limits_{x\in\partial I^5}\textrm{area}(\Phi(x))=4\pi$

Informally, ${\Phi}$ is an element of the “homotopy group” ${\pi_5(\mathcal{S},\mathcal{G})}$ where ${\mathcal{S}}$ is the space of surfaces of ${S^3}$ and ${\mathcal{G}}$ is the space of geodesic spheres of ${S^3}$ . More formally, Fernando and André discuss in Sections 7 and 8 of their article (see, in particular, Theorem 8.1) the fact that the min-max family ${\Phi}$ associated to ${\Sigma\subset S^3}$ “naturally” determines a homotopy class ${\Pi}$ called min-max homotopy class associated to ${\Sigma}$ .

At this stage, one would like to prove Theorem 2 by applying the Min-Max Theorem 4 to the min-max homotopy class ${\Pi}$ associated to a compact surface ${\Sigma\subset S^3}$ of genus ${g\geq 1}$ . Of course, before doing so, we need, by item (c) above, to check the “barrier” condition

$\displaystyle L(\Pi)>\sup\limits_{x\in\partial I^5}\textrm{area}(\Phi(x))=4\pi, \ \ \ \ \ (3)$

that is, we need to control the width ${L(\Pi)}$ of the min-max homotopy class ${\Pi}$ . The next two subsections are dedicated to this discussion of this issue.

2.5. Degree of ${\overline{Q}:S^3\rightarrow S^3}$

Recall that during the blow-up procedure (see Subsection 2), we introduced a map ${\overline{Q}:S^3\rightarrow S^3}$ with ${C(v,s(v))=\partial B_{\pi/2}(\overline{Q}(v))}$ .

The main topological ingredient towards the estimate of ${L(\Pi)}$ is the following result (see Theorem 3.7 of the article of Fernando and André):

Theorem 5 The map ${\overline{Q}:S^3\rightarrow S^3}$ is continuous and its degree equals the genus ${g}$ of ${\Sigma\subset S^3}$ .

Below we sketch the calculation of the degree of ${\overline{Q}}$ referring to the original article for the details.

Proof: It is possible to check that:

${\overline{Q}(v)=T(v)}$ if ${v\in A^{ext}-\overline{\Omega_{\varepsilon}}}$ ;
${\overline{Q}(v)=-T(v)}$ if ${v\in A^{int}-\overline{\Omega_{\varepsilon}}}$ ;
${\overline{Q}(v)=\overline{Q}(\Lambda(p,s_1,s_2))=-\frac{a(s_2)}{\sqrt{1+a(s_2)^2}}p - \frac{1}{\sqrt{1+a(s_2)^2}}N(p)}$ with ${a(s_2)=s_2/\sqrt{\varepsilon^2-s_2^2}}$ if ${v=\Lambda(p,s_1,s_2)\in\overline{\Omega_{\varepsilon}}}$ .

From this point, the continuity of ${\overline{Q}}$ is checked by direct inspection.

On the other hand, for the computation of the degree ${\textrm{deg}(\overline{Q})}$ of ${\overline{Q}}$ , we have to calculate, by definition, the following quantity

$\displaystyle \textrm{deg}(\overline{Q}):=\left(\int_{S^3} \overline{Q}^* dV\right)/\left(\int_{S^3} 1 dV\right)=\frac{1}{2\pi^2}\int_{S^3} \overline{Q}^* dV$

where ${dV}$ is the volume form of ${S^3}$ .

In this direction, one uses that ${T}$ is a (orientation-preserving) diffeomorphism from ${A^{ext}-\overline{\Omega_{\varepsilon}}}$ to ${\overline{A^{ext}}}$ , and from ${A^{int}-\overline{\Omega_{\varepsilon}}}$ to ${\overline{A^{int}}}$ , so that

$\displaystyle \int_{A^{ext}-\overline{\Omega_{\varepsilon}}}\overline{Q}^* dV = \int_{A^{ext}}dV=\textrm{vol}(A^{ext})$

and

$\displaystyle \int_{A^{int}-\overline{\Omega_{\varepsilon}}}\overline{Q}^* dV = \int_{A^{int}}dV=\textrm{vol}(A^{int})$

Since ${\Sigma}$ has zero measure (volume) in ${S^3}$ and ${S^3-\Sigma=A^{int}\cup A^{ext}}$ , we get that

$\displaystyle \int_{S^3-\overline{\Omega_{\varepsilon}}}\overline{Q}^* dV = \textrm{vol}(A^{ext})+\textrm{vol}(A^{int}) = \textrm{vol}(S^3)=2\pi^2.$

Therefore,

$\displaystyle \textrm{deg}(\overline{Q})=1+\frac{1}{2\pi^2}\int_{S^3\cap\overline{\Omega_{\varepsilon}}}\overline{Q}^* dV$

and it remains only to calculate the integral ${\int_{S^3\cap\overline{\Omega_{\varepsilon}}}\overline{Q}^* dV}$ .

Consider ${G:\Sigma\times[-\varepsilon,\varepsilon]\rightarrow S^3\cap\overline{\Omega_{\varepsilon}}}$ , ${G(\Lambda(p,0,t))=\cos(t)p+\sin(t)N(p)}$ . It is not hard to check that ${G}$ is an orientation-preserving diffeomorphism: for instance, by fixing a positive basis ${\{e_1,e_2\}}$ of ${T_p\Sigma}$ , one has ${DG(p,0)\cdot(e_1\wedge e_2\wedge\partial_t)=e_1\wedge e_2\wedge N(p)}$ . So, by putting ${Q = \overline{Q}\circ G}$ ,

$\displaystyle \int_{S^3\cap\overline{\Omega_{\varepsilon}}}\overline{Q}^* dV = \int_{\Sigma\times[-\varepsilon,\varepsilon]}Q^* dV.$

Notice that

$\displaystyle Q(p,t)=-\frac{t}{\varepsilon}p-\frac{\sqrt{\varepsilon^2-t^2}}{\varepsilon}N(p)$

By selecting a positive orthonormal basis ${\{e_1,e_2\}}$ of ${T_p\Sigma}$ diagonalizing the second fundamental form, we have (by definition) that ${\nabla_{e_i} N = -k_i e_i}$ . After some calculations, Fernando and André find that

$\displaystyle \int_{\Sigma\times[-\varepsilon,\varepsilon]}Q^* dV = -\int_{\Sigma}\int_{-\varepsilon}^{\varepsilon}\frac{1}{\varepsilon^2}\left(k_1k_2\sqrt{\varepsilon^2-t^2} - (k_1+k_2)t + \frac{t^2}{\sqrt{\varepsilon^2-t^2}}\right)dt\,d\Sigma$

Because ${\int_{-\varepsilon}^{\varepsilon}t\,dt=0}$ , we obtain

$\displaystyle \int_{\Sigma\times[-\varepsilon,\varepsilon]}Q^* dV = -\int_{\Sigma}\int_{-\varepsilon}^{\varepsilon}\frac{1}{\varepsilon^2}\left(k_1k_2\sqrt{\varepsilon^2-t^2} + \frac{t^2}{\sqrt{\varepsilon^2-t^2}}\right)dt\,d\Sigma$

Since ${\int_{-\varepsilon}^{\varepsilon}\frac{\sqrt{\varepsilon^2-t^2}}{\varepsilon^2}\,dt = \int_{-\pi/2}^{\pi/2}\cos^2\theta\,d\theta = \pi/2}$ and ${\int_{-\varepsilon}^{\varepsilon}\frac{t^2}{\varepsilon^2\sqrt{\varepsilon^2-t^2}}\,dt = \int_{-\pi/2}^{\pi/2}\cos^2\theta\,d\theta = \pi/2}$ , we get

$\displaystyle \int_{\Sigma\times[-\varepsilon,\varepsilon]}Q^* dV = -\frac{\pi}{2}\int_{\Sigma}\left(k_1k_2 + 1\right)\,d\Sigma$

Finally, by Gauss formula, the Gaussian curvature ${K}$ of ${\Sigma\subset S^3}$ is ${K=1+k_1k_2}$ , so that, by Gauss-Bonnet theorem, we have that

$\displaystyle \int_{S^3\cap\overline{\Omega_{\varepsilon}}}\overline{Q}^* dV=\int_{\Sigma\times[-\varepsilon,\varepsilon]}Q^* dV = -\frac{\pi}{2}\int_{\Sigma} K \,d\Sigma = -\pi^2\chi(\Sigma)=2\pi^2(g-1)$

Plugging this equation in the formula for the degree of ${\overline{Q}}$ derived above, we conclude that

$\displaystyle \textrm{deg}(\overline{Q})=1+\frac{1}{2\pi^2}\int_{S^3\cap\overline{\Omega_{\varepsilon}}}\overline{Q}^* dV = g.$

This completes the sketch of proof of the theorem. $\Box$

This topological theorem has the following nice homological consequence. As we mentioned in Subsection 2 (see item (a)), the min-max family ${\Phi}$ satisfies ${|\Phi|(\widetilde{x},1/2)=\partial B_{\pi/2}(\overline{Q}(f(\widetilde{x})))\in\mathcal{T}}$ for all ${\widetilde{x}\in\partial I^4}$ , where ${\mathcal{T}}$ denotes the set of all unoriented totally geodesic spheres of ${S^3}$ and ${|\Phi|(x)}$ is the surface ${\Phi(x)}$ without a choice of orientation. Note that ${\mathcal{T}}$ is naturally isomorphic to the real projective space ${\mathbb{RP}^3}$ by associating to each geodesic sphere ${\partial B_{\pi/2}(p)}$ the line ${\mathbb{R}p}$ passing by its center.

In other words, the map ${|\Phi|}$ (derived from ${\Phi}$ by forgetting orientations) sends ${\partial I^4\times\{1/2\}}$ to ${\mathcal{T}}$ . Moreover, since ${|\Phi|(\widetilde{x},1/2)=\partial B_{\pi/2}(\overline{Q}(f(\widetilde{x})))}$ , ${\textrm{deg}(\overline{Q})=g}$ (and the natural map ${S^3\rightarrow\mathbb{RP}^3}$ has degree ${2}$ ), we have the following crucial homological fact

$\displaystyle |\Phi|_*(\partial I^4\times\{1/2\})=2g\in H_3(\mathbb{RP}^3,\mathbb{Z}) \ \ \ \ \ (4)$

In the next subsection, we will use this fact to control the width of the min-max homotopy classes and complete the proof of Theorem 2.

2.6. The width of min-max homotopy classes

In this subsection we will consider ${\Sigma\subset S^3}$ a compact surface of genus ${g\geq 1}$ , so that, by Equation (4),

$\displaystyle 0\neq2g= |\Phi|_*(\partial I^4\times\{1/2\})\in H_3(\mathbb{RP}^3,\mathbb{Z}) \ \ \ \ \ (5)$

and we want to get that the width ${L(\Pi)}$ of the min-max homotopy class associated to ${\Sigma}$ satisfies ${L(\pi)>4\pi}$ . Compare with Theorem 9.1. Of course, once we proved this, the proof of Theorem 2 is complete because (in view of the discussion in Subsection 2) ${L(\Pi)>4\pi}$ is precisely the “barrier” condition one needs to apply the Min-Max Theorem 4.

The proof of ${L(\Pi)>4\pi}$ goes by contradiction: suppose that ${L(\Pi)\leq 4\pi}$ and consider a sequence ${\{\phi_i\}_{i\in\mathbb{N}}\subset\Pi}$ with

$\displaystyle \sup\limits_{x\in I^5}\textrm{area}(\phi_i(x))\leq 4\pi+1/i$

By the definition of the homotopy classes, one also has ${\phi_i(x)=\Phi(x)}$ for all ${x\in\partial I^5}$ and ${i\in\mathbb{N}}$ .

Fix ${\varepsilon>0}$ small and let ${\widetilde{A}(i)}$ be the set of ${x\in I^5}$ such that ${\phi_i(x)}$ is “ ${\varepsilon}$ -far” (in an appropriate sense in the space of currents) from the set ${\mathcal{T}}$ of totally geodesic spheres of ${S^3}$ . Since ${\phi_i(x)=\Phi(x)}$ is a trivial (zero area) surface for every ${x\in (I^4\times\{0\})\cup(I^4\times\{1\})}$ , we have that ${\widetilde{A}(i)\supset (I^4\times\{0\})\cup(I^4\times\{1\})}$ . Let ${A(i)}$ denote the connected component of ${\widetilde{A}(i)}$ containing ${I^4\times\{0\}}$ . For sake of simplicity of the exposition, we will assume that ${\widetilde{A}(i)}$ and ${A(i)}$ are compact manifolds with boundary.

We start by showing that ${A(i)\cap(I^4\times\{1\})=\emptyset}$ for all ${i}$ large. Assume that this is not the case. Then, one can find a sequence of continuous paths ${\gamma_i:[0,1]\rightarrow A(i)}$ with ${\gamma_i(0)\in I^4\times\{0\}}$ and ${\gamma_i(1)\in I^4\times\{1\}}$ . The maps ${\sigma_i = \phi_i\circ \gamma_i}$ defined on ${I=[0,1]}$ are mutually homotopic and their homotopy class ${\Pi_{(0)}}$ is very similar to the homotopy class ${\Pi_0}$ of Example 1. In particular, the width of ${L(\Pi_{(0)})}$ is ${L(\Pi)=4\pi(=L(\Pi_0))}$ .

Thus, we have

$\displaystyle 4\pi=L(\Pi_{(0)})\leq\sup\limits_{t\in I}\textrm{area}(\sigma_i(t))\leq \sup\limits_{x\in I^5}\textrm{area}(\phi_i(t))\leq 4\pi+1/i.$

Since ${\sigma_i(0)}$ and ${\sigma_i(1)}$ are trivial surfaces, we can apply the Min-Max Theorem 4to produce a sequence ${t_i\in I}$ such that ${\sigma_i(t_i)}$ converges to a minimal surface ${S}$ of ${S^3}$ of area ${4\pi}$ . From our discussion in the introduction, ${S}$ must be a totally geodesic sphere, and this is a contradiction with the definition of ${\widetilde{A}(i)}$ , i.e., ${\sigma_i(t_i)}$ is “ ${\varepsilon}$ -far” from the set ${\mathcal{T}}$ of totally geodesic spheres.

Now, since ${A(i)\cap(I^4\times\{1\})=\emptyset}$ for all ${i}$ large, we have that

$\displaystyle \partial A(i)\cap\partial I^5 \subset (\partial I^4\times I) \cup (I^4\times\{0\}).$

Consider the ${4}$ -dimensional submanifold ${R(i):=\partial A(i)\cap \textrm{int}(I^5)}$ . By definition of ${A(i)}$ , for any ${x\in R(i)}$ , ${\phi_i(x)}$ is “ ${\varepsilon}$ -close” (i.e., not “ ${\varepsilon}$ -far”) from the set ${\mathcal{T}}$ of totally geodesic spheres. On the hand, trivial surfaces are “ ${\varepsilon}$ -far” from ${\mathcal{T}}$ , and the image of ${I^4\times\{0\}}$ under ${\phi_i}$ (or equivalently ${\Phi}$ ) consists of trivial (zero area) surfaces. Putting this together with the set inclusion of the previous paragraph, we deduce that

$\displaystyle \partial R(i)\subset \partial I^4\times I$

In resume, ${R(i)}$ is a ${4}$ -dimensional submanifold separating ${I^4\times\{0\}}$ from ${I^4\times\{1\}}$ . Furthermore, by item (a) in Subsection 2, for all ${\widetilde{x}\in\partial I^4}$ , ${\Phi(\widetilde{x},t)}$ is a totally geodesic sphere if and only if ${t=1/2}$ . Hence, given ${\delta>0}$ , we can select ${\varepsilon>0}$ small so that

$\displaystyle \partial R(i)\subset \partial I^4\times [1/2-\delta,1/2+\delta].$

We claim that ${\partial R(i)}$ is homologous to ${\partial I^4\times\{1/2\}}$ in ${\partial I^4\times I}$ . Indeed, define ${C(i):=\partial A(i)\cap (\partial I^4\times I)}$ . Since ${\partial A(i)}$ has no boundary, one has

$\displaystyle \partial C(i) = \partial R(i)\cup(\partial I^4\times\{0\}).$

In particular, since ${C(i)\subset \partial I^4\times I}$ , we conclude that ${\partial R(i)}$ is homologous to ${\partial I^4\times \{0\}}$ in ${\partial I^4\times I}$ . Hence, ${\partial R(i)}$ is also homologous to ${\partial I^4\times \{1/2\}}$ in ${\partial I^4\times I}$ , as it was claimed.

Finally, we consider the map ${\widehat{\Phi}(x,t):=|\Phi|(x,1/2)\in\mathcal{T}}$ associating to ${(x,t)\in\partial I^4\times I}$ the unoriented totally geodesic sphere ${|\Phi|(x,1/2)}$ . Because ${\phi_i=\Phi}$ on ${\partial I^5}$ (by definition of the homotopy class ${\Pi}$ ) and ${\partial R(i)\subset \partial I^4\times [1/2-\delta,1/2+\delta]}$ (see above), we have that ${\phi|_{\partial R(i)}}$ is “ ${\varepsilon}$ -close” to ${\widehat{\Phi}|_{\partial R(i)}}$ . Using this and the fact that ${\phi_i(x)}$ is “ ${\varepsilon}$ -close” to ${\mathcal{T}}$ for ${x\in R(i)}$ (see the definition of ${R(i)}$ above), Fernando and André construct a continuous map ${f_i:R(i)\rightarrow\mathcal{T}}$ from the ${4}$ -dimensional manifold ${R(i)}$ to ${\mathcal{T}\simeq\mathbb{RP}^3}$ approximating ${\phi_i}$ on ${R(i)}$ such that ${f_i=\widehat{\Phi}}$ on ${\partial R(i)}$ (see Lemma 9.10 of their article). In homology, this implies that

$\displaystyle \widehat{\Phi}_*[\partial R(i)] = (f_i)_*[\partial R(i)]=[\partial ((f_i)_{\#}(R(i))]=0$

However, we just saw that ${\partial R(i)}$ is homologous to ${\partial I^4\times \{1/2\}}$ . Hence, by the topological result in Equation 5 above,

$\displaystyle \widehat{\Phi}_*[\partial R(i)] = \widehat{\Phi}_*[\partial I^4\times\{1/2\}] = |\Phi|_*(\partial I^4\times)=2g\neq0\in H_3(\mathbb{RP}^3,\mathbb{Z})$

when ${g\geq 1}$ .

Of course this is a contradiction showing that the width ${L(\Pi)}$ of min-max homotopy classes ${\Pi}$ of surfaces ${\Sigma\subset S^3}$ of genus ${g\geq 1}$ verify ${L(\Pi)>4\pi}$ .

For more details on the arguments of this subsection, we refer the reader to Section 9 of the article of Fernando and André. Now, we pass to the discussion of the proof of Theorems 3 and 1.

3. Strategy of the proof of Theorem 3

Before starting our considerations, we introduce the notion of (stability) index of a compact surface ${\Sigma\subset S^3}$ . We denote by ${\Delta}$ the Laplace-Beltrami operator, ${A}$ the second fundamental form and ${L=\Delta+|A|^2+2}$ the Jacobi operator of ${\Sigma\subset S^3}$ . The index ${\textrm{index}(\Sigma)}$ of ${\Sigma}$ is the number of negative eigenvalues of ${L}$ . For a discussion of the index and second variation formulas for surfaces, see e.g. this post of Danny Calegari.

As it is explained in Appendix A of the article of Fernando and André, one can always find a minimal surface ${\Sigma\subset S^3}$ of genus ${g\geq 1}$ of least area among all minimal surfaces of ${S^3}$ with genus ${g\geq 1}$ . Because the Clifford torus ${\Sigma_c}$ has area ${2\pi^2}$ , we have that ${\textrm{area}(\Sigma)\leq 2\pi^2}$ . Consider the min-max family ${\Phi}$ associated to ${\Sigma}$ and denote by ${\Pi}$ the corresponding min-max homotopy class.

By a theorem of F. Urbano, it suffices to show that ${\textrm{index}(\Sigma)\leq 5}$ to conclude that ${\Sigma}$ is isometric to the Clifford torus ${\Sigma_c}$ (see also Remark 4 above). In other words, the proof of Theorem 3 is reduced to the proof of the estimate ${\textrm{index}(\Sigma)\leq 5}$ . We argue by contradiction. Suppose that ${\textrm{index}(\Sigma)\geq 6}$ and consider the canonical family ${\Sigma_{(v,t)}}$ , ${(v,t)\in B^4\times [-\pi,\pi]}$ associated to ${\Sigma}$ (see Subsection 2). Recall that the canonical family satisfies

$\displaystyle \sup\limits_{(v,t)\in B^4\times [-\pi,\pi]}\textrm{area}(\Sigma_{(v,t)})\leq\mathcal{W}(\Sigma)$

Also, since ${\Sigma}$ is a minimal surface, ${\mathcal{W}(\Sigma)=\textrm{area}(\Sigma)}$ . So,

$\displaystyle \sup\limits_{(v,t)\in B^4\times [-\pi,\pi]}\textrm{area}(\Sigma_{(v,t)})\leq \textrm{area}(\Sigma).$

Moreover, since ${\Sigma}$ is a minimal surface, the function ${(v,t)\mapsto \textrm{area}(\Sigma_{(v,t)})}$ has a global isolated maximum at ${(0,0)}$ . Because ${B^4\times[-\pi,\pi]}$ is ${5}$ -dimensional and we’re assuming that ${\textrm{index}(\Sigma)\geq 6}$ , one can (slightly) perturb ${\Sigma_{(v,t)}}$ near ${(0,0)}$ to produce a new family ${\widetilde{\Sigma}_{(v,t)}}$ with

$\displaystyle \sup\limits_{(v,t)\in B^4\times [-\pi,\pi]}\textrm{area}(\widetilde{\Sigma}_{(v,t)})<\textrm{area}(\Sigma) \ \ \ \ \ (6)$

See Section 10 of the article of Fernando and André for more details.

Now we consider the min-max family ${\widetilde{\Phi}}$ and the min-max homotopy class associated to ${\widetilde{\Sigma}_{(v,t)}}$ . Since the (small) perturbation of ${\Sigma_{(v,t)}}$ is performed near ${(0,0)}$ , one has that

${\widetilde{\Phi}}$ coincides with ${\Phi}$ on ${\partial I^5}$
by Theorem 2, ${L(\widetilde{\Pi})>4\pi}$ (as ${\Sigma}$ has genus ${g\geq 1}$ )
furthermore, there exists a minimal surface ${\widehat{\Sigma}\subset S^3}$ such that
$\displaystyle 4\pi<\textrm{area}(\widehat{\Sigma})=L(\widetilde{\Pi})$

Actually, the minimal surface ${\widehat{\Sigma}}$ provided by Theorem 2 in principle may be not connected and/or may have multiplicity (because Theorem 2 was deduced from the Min-Max Theorem 4). But, by Equation (6),

$\displaystyle 4\pi<\textrm{area}(\widehat{\Sigma})=L(\widetilde{\Pi})\leq \sup\limits_{x\in I^5}\textrm{area}(\widetilde{\Phi}(x))<\textrm{area}(\Sigma)\leq 2\pi^2<8\pi$

Because the area of any minimal surface of ${S^3}$ is ${4\pi}$ at least, and round spheres are precisely the minimal surface of ${S^3}$ with area ${4\pi}$ , it follows from the estimate ${4\pi<\textrm{area}(\widehat{\Sigma})<8\pi}$ above that ${\widehat{\Sigma}}$ is a connected minimal surface of genus ${g\geq 1}$ and multiplicity ${1}$ . On the other hand, ${\Sigma}$ was chosen to minimize the area among all minimal surfaces of ${S^3}$ of genus ${g\geq 1}$ , so that we get ${\textrm{area}(\Sigma)\leq \textrm{area}(\widehat{\Sigma})}$ . Of course, this is a contradiction with the estimate ${\textrm{area}(\widehat{\Sigma})< \textrm{area}(\Sigma)}$ above, and thus ${\textrm{index}(\Sigma)\leq 5}$ as desired. Now that the sketch of proof of Theorem 3 is complete, we close today’s post with the sketch of the proof of Theorem 1.

4. Strategy of the proof of Theorem 1

Given ${\Sigma}$ an embedded compact surface of ${S^3}$ with genus ${g\geq 1}$ . Our goal is to prove that ${\mathcal{W}(\Sigma)\geq 2\pi^2}$ . Because ${2\pi^2<8\pi}$ , we can assume (without loss of generality) that ${\mathcal{W}(\Sigma)<8\pi}$ . Denote by ${\Phi}$ the min-max family and ${\Pi}$ the min-max homotopy class associated to ${\Sigma}$ . By Theorem 2, we have that

$\displaystyle 4\pi<L(\Pi)=\textrm{area}(\widehat{\Sigma})\leq\mathcal{W}(\Sigma)<8\pi$

where ${\widehat{\Sigma}\subset S^3}$ is a minimal surface (maybe not connected and possibly with multiplicities). By the same arguments of the last paragraph of the previous section, the fact ${4\pi<\textrm{area}(\widehat{\Sigma})<8\pi}$ implies that ${\widehat{\Sigma}}$ is a connected minimal surface with genus ${g\geq 1}$ and multiplicity ${1}$ . By Theorem 3, we have ${\textrm{area}(\widehat{\Sigma})\geq 2\pi^2}$ . Thus, we get

$\displaystyle \mathcal{W}(\Sigma)\geq \textrm{area}(\widehat{\Sigma})=2\pi^2$

and the first part of the statement of Theorem 1is proved.

Finally, concerning the second (“rigidity”) part of the statement of Theorem 1, given a compact surface ${\Sigma}$ of genus ${g\geq 1}$ with ${\mathcal{W}(\Sigma)=2\pi^2}$ , one considers the conformal transformations ${F_v}$ introduced in Subsection 2 and one starts the argument by proving that there exists ${v\in B^4}$ with ${\textrm{area}(F_v(\Sigma))=\mathcal{W}(\Sigma)=2\pi^2}$ . Here, the proof of this fact goes by contradiction: by supposing that ${\textrm{area}(F_v(\Sigma))<2\pi^2}$ for all ${v\in B^4}$ , one can approach the boundary ${\partial B^4}$ along a subsequence ${v_i\in B^4}$ to produce a totally geodesic sphere ${S}$ contained in the minimal surface ${\widehat{\Sigma}}$ constructed above, but this is not possible because ${\widehat{\Sigma}}$ has genus ${g\geq 1}$ . Then, once we know that ${\textrm{area}(F_v(\Sigma))=2\pi^2}$ for some ${v\in B^4}$ , we have by Theorem 3 that ${F_v(\Sigma)}$ is isometric to the Clifford torus, that is, ${\Sigma}$ is conformal to the Clifford torus.

Posted in expository, math.DG, Mathematics | Tags: Almgren-Pitts Min-Max Theory, Andre Neves, Clifford torus, conformal transformations, Fernando Coda Marques, Min-Max Theorem, Width of homotopy classes, Willmore conjecture

Responses

thanks for your interpolation this article. I have bee reading it.
By: yearlie on June 13, 2012
at 1:29 pm

Reply
I have translate it to my site:http://lttt.blog.ustc.edu.cn/2012/07/16/fernando-coda-marques%e4%b8%8eandre-neves-%e8%a7%a3%e5%86%b3willmore%e7%8c%9c%e6%83%b3-2.html
By: van abel on August 6, 2013
at 5:12 am

Reply
what software do you use to make such figures ?
By: Allain on August 22, 2013
at 3:29 am

Reply

	Adam on Breuillard-Sert’s joint…
	Adam on Breuillard-Sert’s joint…
	Writing a Hilbert C*… on ERT16: Compact extensions
	matheuscmss on Yoccoz book collection at…
	Jairo B. on Yoccoz book collection at…

Disquisitiones Mathematicae