Posted by: matheuscmss | May 10, 2015

The Hausdorff measure (at adequate scale) of simply connected planar domains

Some of the partial advances obtained by Jacob Palis, Jean-Christophe Yoccoz and myself on the computation of Hausdorff dimensions of stable and unstable sets of non-uniformly hyperbolic horseshoes (announced in this blog post here and this survey article here) are based on the following lemma:

Lemma 1 Let {f:B\rightarrow\mathbb{R}^2} be a {C^1} diffeomorphism from the closed unit ball {B:= \{(x,y)\in\mathbb{R}^2: x^2 + y^2\leq 1\}} of {\mathbb{R}^2} into its image.Let {K\geq 1} and {L\geq 1} be two constants such that {\|Df(p)\|\leq K} and {\textrm{Jac}(f)(p):=|\det Df(p)|\leq L} for all {p\in B}.

Then, for each {1\leq d\leq 2}, the {d}-dimensional Hausdorff measure {H^d_{\sqrt{2}}(f(B))} at scale {\sqrt{2}} of {f(B)} satisfies

\displaystyle H^d_{\sqrt{2}}(f(B)) := \inf\limits_{\substack{\bigcup\limits_{i\in \mathbb{N}} U_i \supset f(B), \\ \textrm{diam}(U_i)\leq \sqrt{2}}}\sum\limits_{i\in\mathbb{N}}\textrm{diam}(U_i)^d \leq 170\pi \cdot \max\{K,L\}^{2-d} \cdot L^{d-1} \ \ \ \ \ (1)

Remark 1 In fact, this is not the version of the lemma used in practice by Palis, Yoccoz and myself. Indeed, for our purposes, we need the estimate

\displaystyle H^d_{r\sqrt{2}}(g(B_r))\leq 170\pi\cdot r^d\cdot K^{2-d}\cdot L^{d-1}

where {B_r} is the ball of radius {r} centered at the origin and {g} is a {C^1} diffeomorphism such that {\|Dg\|\leq K} and {\textrm{Jac}(g)\leq L} for {1\leq L\leq K}. Of course, this estimate is deduced from the lemma above by scaling, i.e., by applying the lemma to {f = h_r^{-1}\circ g\circ h_r } where {h_r:\mathbb{R}^2\rightarrow\mathbb{R}^2} is the scaling {h_r(p)=rp}.

Nevertheless, we are not completely sure if we should write down an article just with our current partial results on non-uniformly hyperbolic horseshoes because our feeling is that these results can be significantly improved by the following heuristic reason.

In a certain sense, Lemma 1 says that one of the “worst” cases (where the estimate (1) becomes “sharp” [modulo the multiplicative factor {170\pi}]) happens when {f} is an affine hyperbolic conservative map {f_K(x,y)=(Kx,\frac{1}{K}y)} (say {K\geq 1}): indeed, since {[-\sqrt{\frac{1}{2}}, \sqrt{\frac{1}{2}}]\times [-\sqrt{\frac{1}{2}}, \sqrt{\frac{1}{2}}]\subset B\subset [-1,1]\times [-1,1]}, the most “economical” way to cover {f_K(B)} using a countable collection of sets of diameters {\leq \sqrt{2}} is basically to use {K^2} squares of sizes {1/K} (which gives an estimate {H^d_{\sqrt{2}}(f(B))\leq K^2(1/K)^d = K^{2-d}}).

However, in the context of (expectional subsets of stable sets of) non-uniformly hyperbolic horseshoes, we deal with maps {f} obtained by successive compositions of affine-like hyperbolic maps and a certain folding map (corresponding to “almost tangency” situations). In particular, we work with maps {f} which are very different from affine hyperbolic maps and, thus, one can expect to get slightly better estimates than Lemma 1 in this setting.

In summary, Jacob, Jean-Christophe and I hope to improve the results announced in this survey here, so that Lemma 1 above will become a “deleted scene” of our forthcoming paper.

On the other hand, this lemma might be useful for other purposes and, for this reason, I will record its (short) proof in this post.

1. Proof of Lemma 1 

The proof of (1) is based on the following idea. By studying the intersection of {f(B)} with dyadic squares on {\mathbb{R}^2}, we can interpret the measure {H^d_{\sqrt{2}}(f(B))} as a sort of {L^d}-norm of a certain function. Since {1\leq d\leq 2}, we can control this {L^d}-norm in terms of the {L^1} and {L^2} norms (by interpolation). As it turns out, the {L^1}-norm, resp. {L^2}-norm, is controlled by the features of the derivative {Df}, resp. Jacobian determinant {Jac(f)}, and this morally explains the estimate (1).

Let us now turn to the details of this argument. Denote by {U:=f(B)} and {\partial U} its boundary. For each integer {k\geq 0}, let {\Delta_k} be the collection of dyadic squares of level {k}, i.e., {\Delta_k} is the collection of squares of sizes {1/2^k} with corners on the lattice {(1/2^k)\cdot\mathbb{Z}^2}.

Consider the following recursively defined cover of {U}. First, let {\mathcal{C}_0} be the subset of squares {Q\in \Delta_0} such that

\displaystyle \textrm{area}(Q\cap U)\geq \frac{1}{5}

Next, for each {k>0}, we define inductively {\mathcal{C}_k} as the subset of squares {Q\in\Delta_k} such that {Q} is not contained in some {Q'\in\mathcal{C}_l} for {0\leq l < k}, and {Q} intersects a significant portion of {U} in the sense that

\displaystyle \textrm{area}(Q\cap U)\geq \frac{1}{5}\textrm{area}(Q) \ \ \ \ \ (2)

In other words, we start with {U} and we look at the collection {\mathcal{C}_0} of dyadic squares of level {0} intersecting it in a significant portion. If the squares in {\mathcal{C}_0} suffice to cover {U}, we stop the process. Otherwise, we consider the dyadic squares of level {0} not belonging to {\mathcal{C}_0}, we divide each of them into four dyadic squares of level {1}, and we build a collection {\mathcal{C}_1} of such dyadic squares of level {1} intersecting in a significant way the remaining part of {U} not covered by {\mathcal{C}_0}, etc.

Remark 2 In this construction, we are implicitly assuming that {U=f(B)} is not entirely contained in a dyadic square {Q\in\bigcup\limits_{k=0}^{\infty}\Delta_k}. In fact, if {U\subset Q}, then the trivial bound {H^d_{\sqrt{2}}(U)\leq \textrm{diam}(Q)^d\leq (\sqrt{2})^d\leq 2} (for {1\leq d\leq 2}) is enough to complete the proof of the lemma.

In this way, we obtain a countable collection {\bigcup\limits_{k=0}^{\infty} \mathcal{C}_k:=(U_i)_{i\in\mathbb{N}}} covering {U=f(B)} such that {\textrm{diam}(U_i)\leq \sqrt{2}} and

\displaystyle H^d_{\sqrt{2}}(f(B))\leq \sum\limits_{i}\textrm{diam}(U_i)^d = \sum\limits_{k=0}^{\infty} N_k\left(\frac{1}{2^k}\right)^d \ \ \ \ \ (3)

where {N_k:=(\sqrt{2})^d\#\mathcal{C}_k}.

By thinking of this expression as a {L^d}-norm and by applying interpolation between the {L^1} and {L^2} norms, we obtain that

\displaystyle \sum\limits_{k=0}^{\infty} N_k\left(\frac{1}{2^k}\right)^d\leq \left(\sum\limits_{k=0}^{\infty} \frac{N_k}{2^k}\right)^{2-d} \left(\sum\limits_{k=0}^{\infty} \frac{N_k}{(2^k)^2}\right)^{d-1} \ \ \ \ \ (4)

This reduces our task to estimate these {L^1} and {L^2} norms. We begin by observing that the {L^2}-norm is easily controlled in terms of the Jacobian of {f} (thanks to the condition (2)):

\displaystyle \sum\limits_{k=0}^{\infty} \frac{N_k}{(2^k)^2} = (\sqrt{2})^d\sum\limits_{k}\sum\limits_{Q\in\mathcal{C}_k} \textrm{area}(Q) \ \ \ \ \ (5)

\displaystyle \begin{array}{rcl} &\leq & (\sqrt{2})^d\sum\limits_{k}\sum\limits_{Q\in\mathcal{C}_k} 5\cdot \textrm{area}(Q\cap U) \\ &\leq& 10 \cdot \textrm{area}(U) = 10 \int_B \textrm{Jac}(f) \\ &\leq& 10\pi\cdot L \end{array}

for any {1\leq d\leq 2}. In particular, we have that

\displaystyle N_0\leq 10\pi L

From this estimate, we see that the {L^1}-norm satisfies

\displaystyle \sum\limits_{k=0}^{\infty} \frac{N_k}{2^k} = N_0+\sum\limits_{k=1}^{\infty} \frac{N_k}{2^k}\leq 10\pi L+\sum\limits_{k>0} \frac{N_k}{2^k} \ \ \ \ \ (6)

Thus, we have just to estimate the series {\sum\limits_{k>0} \frac{N_k}{2^k}}. We affirm that this series is controlled by the derivative of {f}. In order to prove this, we need the following claim:

Claim. For each {k>0} and {Q\in\mathcal{C}_k}, one has

\displaystyle \textrm{length}(Q\cap \partial U)\geq \frac{1}{20}\cdot\frac{1}{2^k} \ \ \ \ \ (7)

Proof of Claim. Note that {U} can not contain {Q}: indeed, since {Q\subset Q'} for some dyadic square {Q'\in\Delta_{k-1}} of level {k-1\geq 0} (and, thus, {4\cdot \textrm{area}(Q) = \textrm{area}(Q')}), if {Q\subset U}, then {\textrm{area}(Q'\cap U)\geq \textrm{area}(Q\cap U) = \textrm{area}(Q)=\frac{1}{4}\textrm{area}(Q')}, a contradiction with the definition of {Q\in\mathcal{C}_k}. Because we are assuming that {U} is not contained in {Q} (cf. Remark 2) and we also have that {Q} intersects (a significant portion of) {U}, we get that

\displaystyle \partial U\cap \partial Q\neq \emptyset

For the sake of contradiction, suppose that {\textrm{length}(\partial U\cap Q)<\frac{1}{20\cdot 2^k}}. Since {\partial U} intersects {\partial Q}, the {\frac{1}{20\cdot 2^k}}-neighborhood {V_k} of {\partial Q} contains {\partial U\cap Q}. This means that

  • (a) either {Q-V_k} is contained in {U}
  • (b) or {Q-V_k} is disjoint from {U}

However, we obtain a contradiction in both cases. Indeed, in case (a), we get that a dyadic square {Q'} of level {k-1} containing {Q} satsifies

\displaystyle \textrm{area}(Q'\cap U)\geq \textrm{area}(Q-V_k) = \left(1-2\cdot\frac{1}{20}\right)^2\textrm{area}(Q) = \frac{81}{400}\textrm{area}(Q'),

a contradiction with the definition of {Q\in\mathcal{C}_k}. Similarly, in case (b), we obtain that

\displaystyle \textrm{area}(Q\cap U)\leq \textrm{area}(Q\cap V_k) = \left(1-\frac{81}{100}\right)\textrm{area}(Q) < \frac{1}{5}\textrm{area}(Q),

a contradiction with (2).

This completes the proof of the claim. {\square}

Coming back to the calculation of the series {\sum\limits_{k>0} N_k/2^k}, we observe that the estimate (7) from the claim and the fact that {\|Df\|\leq K} imply:

\displaystyle \begin{array}{rcl} \sum\limits_{k>0} \frac{N_k}{2^k} &=& (\sqrt{2})^d \sum\limits_{k>0}\sum\limits_{Q\in\mathcal{C}_k} \frac{1}{2^k} \\ &\leq& 20(\sqrt{2})^d\sum\limits_{k>0}\sum\limits_{Q\in\mathcal{C}_k}\textrm{length}(\partial U\cap Q) \\ &\leq& 20(\sqrt{2})^d 2 \cdot \textrm{length}(\partial U) \\ &\leq& 80 K\cdot \textrm{length}(\partial B) = 160\pi K \end{array}

By plugging this estimate into (6), we deduce that the {L^1}-norm verifies

\displaystyle \sum\limits_{k=0}^{\infty} \frac{N_k}{2^k}\leq 170\pi \max\{K,L\} \ \ \ \ \ (8)

Finally, from (3), (4), (5) and (8), we conclude that

\displaystyle H^d_{\sqrt{2}}(f(B))\leq (170\pi)^{2-d}(10\pi)^{d-1}\max\{K,L\}^{2-d} L^{d-1}\leq 170\pi \max\{K,L\}^{2-d} L^{d-1}

This ends the proof of the lemma.

Posted in expository, math.DS, Mathematics | Tags: , , , , ,

«
»

Responses

  1. What kind of diffeomorphisms you have in mind? Can you name an example of a diffeomorphism of the disk where Lemma 1 gives a non-trivial result? In fact, map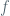 f where I can write the equation or compute 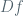Df will be pretty boring. I am not a dynamicist so I can’t think of many examples.

    Even though the image is topologially a disk and the boundary is a differentiable, the boundary might be very complicated.

    By: MrCactu5 (@MonsieurCactus) on May 11, 2015
    at 8:46 pm

    Reply

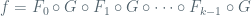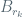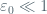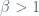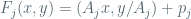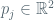    • A prototype of the kind of diffeomorphisms that we have in mind is f = F_0\circ G\circ F_1\circ G\circ\dots\circ F_{k-1}\circ G defined on a ball B_{r_k} of doubly exponentially small radius r_k (i.e., r_k\sim \varepsilon_0^{\beta^k} for some \varepsilon_0\ll 1, \beta>1) “near” to the origin, where F_j(x,y)=(A_j x, y/A_j)+ p_j is an affine hyperbolic diffeomorphism (with A_j\gg 1 and p_j\in\mathbb{R}^2 “close” to the origin), and 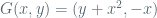G(x,y) = (y+x^2, -x) is a folding map (given by the composition of a fold (x,y)\mapsto (x, y+x^2) and a rotation (x,y)\mapsto (y,-x)).

      Here, the point is that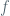 f is a “complicated” map (algebraic map of degree 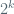2^k whose coefficients depend on parameters A_j, p_j), but one can estimate the Hausdorff measure (at scale r_k) of f(B_{r_k}) thanks to (the remark after) Lemma 1.

      Indeed,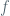 f is area-preserving, and, furthermore, one can give a better bound to the derivative of 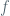f than the trivial bound

      |Df|\leq C^k A_{k-1}\dots A_0

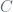      (where C is a bound for the derivative of the folding map 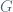G) because the derivative of the folding map 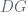DG “tends” to send (with some “parabolic” effect) the (horizontal) direction of maximal expansion for 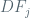DF_j to (almost vertical) directions of almost maximal contraction for 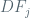DF_j, and vice-versa. In particular, by performing the calculation of 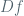Df using this observation, one can show that

      |Df|\leq C^k A_{k-1}\sqrt{A_{k-2}\dots A_0}

      and this is the one of the important inputs used by Jacob, Jean-Christophe and I in our dynamical applications of the lemma.

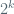      I hope this explains why the lemma helps us in this setting (coming from dynamics): we want to estimate the Hausdorff measure (at fixed scale r_k) of a set f(B_{r_k}) with complicated geometry (of “algebraic complexity” 2^k); instead of looking at the fine details of the geometry of this set, the lemma tells us that one can reasonably estimate the Hausdorff measure (at fixed scale) if there is a “dynamical reason” forcing the derivative and Jacobian of 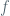f to satisfy some better bounds than the “trivial” ones.

      In other terms, the lemma gives you good geometrical information (Hausdorff measure, optimal covers of sets) if you dispose of good dynamical/analytical information (non-trivial bounds on derivative and/or Jacobian).

      By: matheuscmss on May 12, 2015
      at 9:42 am

      Reply


Leave a comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.

Categories