Last week, my friends Fernando and André uploaded to the arXiv their remarkable paper “Denseness of minimal hypersurfaces for generic metrics” joint with Kei Irie (and, in fact, Fernando sent me a copy of this article about one day before arXiv’s public announcement).
The motivation for the work of Irie–Marques–Neves is a famous conjecture of Yau on the abundance of minimal surfaces.
More precisely, Yau conjectured in 1982 that a closed Riemannian -manifold contains infinitely many (smooth) closed immersed minimal surfaces. Despite all the activity around this conjecture, the existence of infinitely many embedded minimal hypersurfaces in manifolds of positive Ricci curvature
of low dimensions
was only established very recently by Fernando and André.
In their remarkable paper, Irie–Marques–Neves show that Yau’s conjecture is generically true in low dimensions by establishing the following stronger statement:
Theorem 1 Let
be a closed manifold of dimension
. Then, a generic Riemannian metric
on
has a lot of minimal hypersurfaces: the union of all of its closed (smooth) embedded minimal hypersurfaces is a dense subset of
.
Remark 1 The hypothesis
of low dimensionality is related to the fact that area-minimizing minimal hypersurfaces in dimensions
might exhibit non-trivial singular sets (as it was famously proved by Bombieri–De Giorgi–Guisti), but such a phenomenon does not occur in low dimensions for “min-max” minimal hypersurfaces thanks to the regularity theories of Almgren, Pitts and Schoen–Simon.
The remainder of this post is dedicated to the proof of this theorem and, as usual, all eventual errors/mistakes in what follows are my entire responsibility.
1. Description of the key ideas
Let be a closed manifold and
be the space of
Riemannian metrics on
.
Given an open subset , let
be the subset of Riemannian metrics
possessing a non-degenerateclosed (smooth) embedded minimal hypersurface passing through
. (Here, non-degenerate means that all Jacobi fields are trivial.)
It is possible to check that a non-degenerate closed embedded minimal hypersurface in
is persistent: more concretely, one can use the definition of non-degeneracy and the inverse function theorem to obtain that any Riemannian metric
close to
possesses an unique closed embedded minimal hypersurface
nearby
. In particular, every
is open.
Also, let us observe (for later use) that the non-degeneracy condition is not difficult to obtain:
Proposition 2 Let
be a closed (smooth) embedded minimal hypersurface in the Riemannian manifold
. Then, we can perform conformal perturbations to find a sequence of metrics
converging to
(in
-topology) such that
is a non-degenerate minimal hypersurface of
for all sufficiently large
.
Proof: This statement is Proposition 2.3 in Irie–Marques–Neves paper and its proof goes along the following lines.
Fix a bump function supported in a small neighborhood of
and coinciding with the square
of the distance function
nearby
.
The metrics are conformal to
, and they converge to
in the
-topology. Furthermore, the features of the distance function imply that
is a minimal hypersurface of
such that the Jacobi operator
acting on normal vector fields verify
for all . In particular, the spectrum of
is derived from the spectrum of
by translation by
. Therefore,
doesn’t belong to the spectrum of
for all
surfficiently large, and, hence,
is a non-degenerate minimal hypersurface of
for all large
.
Coming back to Theorem 1, we affirm that our task is reduced to prove the following statement:
Theorem 3 Let
be a closed manifold of dimension
. Then, for any open subset
, one has that
is dense in
.
In fact, assuming Theorem 3, we can easily deduce Theorem 1: if is a countable basis of open subsets of
, then Theorem 3 ensures that
is a countable intersection of open and dense subsets of the Baire space
; in other terms,
is a residual / generic subset of
such that any
satisfies the conclusions of Theorem 1 (thanks to the definition of
and our choice of
).
Remark 2 Note that, since
is a Baire space, it follows from Baire category theorem that
is a dense subset of
.
Let us now explain the proof of Theorem 3. Given a neighborhood of a smooth Riemannian metric
on a closed manifold
, and an open subset
, our goal is to show that
For this sake, we apply White’s bumpy metric theorem asserting that we can find such that all closed (smooth) immersed minimal hypersurfaces in
are non-degenerate.
If , then we are done. If
, then all closed (smooth) embedded minimal hypersurfaces in
avoid
. In this case, we can naively describe the idea of Irie–Marques–Neves to perturb
to get
as follows:
- we perturb
only in
to obtain
whose volume
is strictly larger than the volume
;
- by the so-called Weyl law for the volume spectrum (conjectured by Gromov and recently proved by Liokumovich–Marques–Neves), the
–widths of
are strictly larger than those of
;
- since
-widths “count” the minimal hypersurfaces, the previous item implies that new minimal hypersurfaces in
were produced;
- because
coincides with
outside
, the minimal hypersurfaces of
avoiding
are the exactly same of
; thus, the new minimal hypersurfaces in
mentioned above must intersect
, i.e.,
.
In the sequel, we will explain how a slight variant of this scheme completes the proof of Theorem 3.
2. Increasing the volume of Riemannian metrics
Let as above. Take
a non-negative smooth bump function supported in
such that
for some
.
Consider the family of conformal deformations of
. Note that
for all
.
From now on, we fix once and for all such that
for all
.
3. Weyl law for the volume spectrum
Roughly speaking, the –width
of a Riemannian manifold
is the following min-max quantity. We consider the space
of closed hypersurfaces of
, and
–sweepouts
of
, i.e.,
is a continuous map from the
-dimensional real projective space
to
which is “homologically non-trivial” and, a fortiori,
is not a constant map.
Remark 3 Intuitively, a
-sweepout
is a non-trivial way of filling
with
-parameter family of hypersurfaces (which is “similar” to the way the
-parameter family of curves
fills the round
-sphere
).
If we denote by the set of
-sweepouts
such that no concentration of mass occur (i.e.,
), then the
-width is morally given by
Remark 4 Formally speaking, the definition of
-width involves more general objects than the ones presented above: we construct
by replacing hypersurfaces by certain
-dimensional flat chains modulo two, we allow arbitrary simplicial complexes
in place of
, etc.: see Irie–Marques–Neves’ paper for more details and/or references.
The -width
varies continuously with
(cf. Lemma 2.1 in Irie–Marques–Neves’ paper). Moreover, it “counts” minimal hypersurfaces (cf. Proposition 2.2 in Irie–Marques–Neves’ paper): if
has dimension
, then, for each
, there is a finite collection
of mutually disjoint, closed, smooth, embedded, minimal hypersurfaces in
with (stability) indices
such that
for some integers . (Here, the stability index is the quantity of negative eigenvalues of the Jacobi operator.)
Furthermore, the asymptotic behavior of is described by Weyl’s law for the volume spectrum (conjectured by Gromov and confirmed by Liokumovich–Marques–Neves): for some universal constant
, one has
In particular, coming back to the context of Section 2, Weyl’s law for the volume spectrum and the fact that has volume strictly larger than
mean that we can select
such that the
-width
is strictly larger than the
-width of
, i.e.,
4. New minimal hypersurfaces intersecting
We affirm that there exists such that
possesses a closed (smooth) embedded minimal hypersurface passing through
.
Otherwise, for each , all closed (smooth) embedded minimal hypersurface in
would avoid
. Since
coincides with
outside
(by construction), the “counting property of
-widths” in equation (1) would imply that
for all .
On the other hand, the fact that is bumpy (in the sense of White’s theorem) permits to conclude that the set
is countable: indeed, a recent theorem of Sharp implies that the collection of connected, closed, smooth embedded minimal hypersurfaces in
with bounded index and volume is finite, so that
is countable.
Since the -width depends continuously on the metric, the countability of
implies that the function
is constant on
. In particular, we would have
a contradiction with (2). So, our claim is proved.
At this point, the argument is basically complete: the metric has a closed (smooth) embedded minimal hypersurface
passing through
; by Proposition 2, we can perturb
(if necessary) in order to get a metric
such that
is a non-degenerate closed (smooth) embedded minimal hypersurface in
, that is,
, as desired.
Hi Carlos,
The restriction dim<8 appears in many of their theorems. How do those examples with singular sets appear? Is there a chance that for generic R. metrics minimal hypersurfaces are actually nice?
By: Andrey on November 9, 2017
at 2:23 pm
Hi Andrey,
Classically, the singular set appears when we try to find area-minimizing hypersurfaces looking like catenoids in Euclidean spaces: if we start in dimension 2 with the four points of coordinates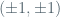 , the area-minimizing “surface” with these points as boundaries is the union of two vertical segments; if we go to three dimensions, the area-minimizing surface passing through the two circles
, the area-minimizing “surface” with these points as boundaries is the union of two vertical segments; if we go to three dimensions, the area-minimizing surface passing through the two circles  is a catenoid rather than a cylinder; in other words, by increasing the dimension, the area-minimizing hypersurface tended to go closer to the origin; if we keep increasing dimensions, then the area-minimizing hypersurface in eight dimension becomes the so-called Simons cone, so that a singularity at the origin pops up.
is a catenoid rather than a cylinder; in other words, by increasing the dimension, the area-minimizing hypersurface tended to go closer to the origin; if we keep increasing dimensions, then the area-minimizing hypersurface in eight dimension becomes the so-called Simons cone, so that a singularity at the origin pops up.
As it turns out, a vast “regularity theory” was developed to explain that this phenomenon of non-trivial singular sets doesn’t occur in dimensions < 8 (and also that singular sets usually have codimension at least 8): see e.g. Ambrosio’s Bourbaki talk for a nice introduction to the subject.
Concerning your last question (about “generic regularity”), I must confess that it is hard for me to give a quick answer (as I’m not an expert on the Almgren–Pitts theory). I will try to consult Fernando on this matter and I will get back to you as soon as possible.
Best,
Matheus
By: matheuscmss on November 9, 2017
at 2:59 pm
Very interesting about the Simons cone, thanks. The boundaries of the cone are some sort of 7d hyperboloids rather than spheres. I guess in the case of spheres singularities don’t form…
By: Andrey on November 9, 2017
at 3:17 pm
Hi Andrey,
I talked to Fernando and he pointed out to me the following facts.
First, it is probably a hard problem to develop a theory of generic singularities in higher dimensions: indeed, such a theory would imply a solution for a notorious well-known open problem, namely, establishing the positive mass theorem (https://en.wikipedia.org/wiki/Positive_energy_theorem) in any dimension. Anyhow, so far one of the best results available in dimension eight is the fact (due to Nat Smale) that the singular set consists of isolated singularities.
Secondly, Fernando believes nevertheless that it could be possible (after *non-trivial* work) to extend the statement of Irie–Marques–Neves theorem by possibly including singular minimal hypersurfaces in the discussion *if* one could generalize White’s bumpy metric theorem for “non-degenerate singular minimal hypersurfaces” (whatever this means…).
Best,
Matheus
By: matheuscmss on November 10, 2017
at 3:27 pm
“First, it is probably a hard problem to develop a theory of generic singularities in higher dimensions: indeed, such a theory would imply a solution for a notorious well-known open problem, namely, establishing the positive mass theorem in any dimension”
I believe the positive mass theorem was proved earlier this year by schoen-yau: https://arxiv.org/abs/1704.05490
By: Lenny G on November 29, 2017
at 4:59 am
Dear Carlos,
Appreciate for the very nice blog for explaining the result and describe the sketch of proof of it!I am curious with both the statement and proof of this result. Unfortunately, I faced some difficulties on understanding the underly idea clearly.
1.
It is easy to see that is open by the property of non-degenerated, I think the subtle thing that why we need to do a small conformal perbutation to make the hyper surface to be non degenerate maybe is in fact this mean the hypersurfaces
is open by the property of non-degenerated, I think the subtle thing that why we need to do a small conformal perbutation to make the hyper surface to be non degenerate maybe is in fact this mean the hypersurfaces  with metric
with metric  could be look as a lots of geodesic segment start form a point
could be look as a lots of geodesic segment start form a point  so there is no topology obstacle because the Jacobi field is trivial, then the openness is just come from a uniformly estimate of a sires of ODE which take charge of the geodesic.
so there is no topology obstacle because the Jacobi field is trivial, then the openness is just come from a uniformly estimate of a sires of ODE which take charge of the geodesic.
2.
So it is suffice to proof dense. Contrasty, we assume there is a metric and a open neiberghood
and a open neiberghood  of
of 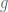 such that
such that  . this result is a corollary of the following two fact on k-width of (M,g) which is the number
. this result is a corollary of the following two fact on k-width of (M,g) which is the number  :
:
We have a representation ,i.e.
,i.e. 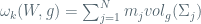 ,
,
These two argument both have subtle details I do not understand fully, the first one is come from the require $\Phi$ is not mass concentrate, I know this is important to establish continuity. But how could we proof this type of ?
?
On the other hand, I could not understand what is the exact meaning of although I know it is come from a definition of maximum-minimum principle so I know look it as some “spectrum”. but how to understand it in a geometric point of view?
although I know it is come from a definition of maximum-minimum principle so I know look it as some “spectrum”. but how to understand it in a geometric point of view? , where
, where 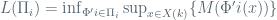 , but I do not understand what is the index of
, but I do not understand what is the index of  and why we still need to use The Compactness Theorem of Sharp to pass to a subsequences?
and why we still need to use The Compactness Theorem of Sharp to pass to a subsequences?
this representation is come from a approximation argument:
I try to understand it but due to I am not very familiar to this area of minimal hyper surface those problem may be very stupid. But I will be very appreciate for an answer.
best,
Xiyu
By: hxypqr on November 13, 2017
at 6:46 pm
Why is there no article on Wikipedia about this important conjecture? xD I would create it my self, but I am not knowledgeable enough. 😦
By: Viktor Kaspervich on December 28, 2017
at 6:55 am
https://en.wikipedia.org/wiki/User_talk:David_Eppstein#Too_advanced_math_for_me
By: Viktor Kaspervich on December 28, 2017
at 11:25 am