Last Wednesday (February 13, 2013) Sylvain Crovisier gave a talk at the Ergodic Theory seminar at LAGA-Paris 13 (that I’m currently helping to organize) about his joint work with Artur Avila and Amie Wilkinson (still not publicly available yet) on the ergodicity of -generic conservative (i.e., volume-preserving) diffeomorphisms.
In his talk, Sylvain presented two of the main results of his work with Avila and Wilkinson (see Theorem 2 and Theorem 3 below), and he sketched the proof of one of them (namely, Theorem 2). Then, after his talk, he told me that he plans to discuss the proof of the other main result next Friday (February 22, 2013) at Eliasson-Yoccoz seminar in Jussieu (University Paris 6 and 7).
So, I will proceed as follows: below I’ll reproduce my notes from Sylvain’s talk at LAGA, and, if I manage to take decent notes from Sylvain’s talk at Jussieu, then I’ll complete today’s discussion (in another post) by sketching the proof of the other main result of Avila-Crovisier-Wilkinson (namely, Theorem 3).
As usual, all mistakes/errors in this post are entirely my responsibility.
1. Setting and statement of main results
Let be a compact, connected manifold (without boundary), and fix
a smooth volume probability measure.
Denote by the set of
-diffeomorphisms of
preserving
.
Our discussion will be “guided” by the following question:
Problem. Is ergodic for “most”
?
Of course, this problem is motivated by the so-called Boltzmann’s ergodic hypothesis “predicting” that the “answer should be yes”.
For , it was shown by J. Oxtoby and S. Ulam that
is ergodic for a
-generic (residual in Baire category sense) conservative homeomorphism.
On the other hand, the celebrated KAM theory shows (in particular) that the analog of Oxtoby-Ulam in higher smoothness is false:
Theorem (Kolmogorov, Arnold, Moser, …, Herman) For
, there exists an open set
such that every
possesses a family of invariant torii
of codimension 1 whose union
is a Cantor set of positive
-volume and the dynamics of
on each invariant torus of this family is
-conjugated to a (irrational) rotation on the standard torus
.
In particular, the dynamics of is not transitive nor ergodic with respect to
.
Remark 1 Some regularity condition for the validity of this theorem is necessary: for example, S. Crovisier and C. Bonatti used their closing lemma for pseudo-orbits to show that the dynamics of a
-generic (in Baire category) conservative diffeomorphism
is transitive. However, the exact regularity threshold
for the validity of Theorem 1 is not known (to the best of my knowledge).
Remark 2 For the sake of our discussion, it is worth to point out that the absence of ergodicity in the open set
of “KAM examples” above is intimately related to the absence of hyperbolicity in the following sense: if
, then
(i.e., there is no future or past exponential growth of the dynamics along the orbit of
) because
is (
-conjugated to) a rotation on
and
preserves a Cantor set lamination transversely to
. In other words, the non-ergodicity of KAM examples is “natural” because they have no non-zero Lyapunov exponents along the orbits in
.
Concerning Remark 2 above, let us recall that, in general, the Oseledets theorem asserts that, for -a.e.
, there is a decomposition into Oseledets subspaces
and a collection of numbers such that
whenever .
From the dynamical point of view, it is natural to distinguish three types of vectors in depending on whether they are exponentially contracted, not exponentially contracted nor expanded, and exponentially expanded, that is,
where ,
and
. We will call
,
and
the stable, central and unstable Oseledets subspaces (resp.).
In this language, we say that is non-uniformly hyperbolic (in the sense of Pesin’s theory) if
for
-a.e.
.
Here, the nomenclature “non-uniform hyperbolicity” is justified by the fact that the conditions or
on Lyapunov exponents provide only asymptotic information on contraction or expansion, so that the time one has to wait before actually getting contraction or expansion might depend heavily on
.
For sake of comparison, let us recall that is called Anosov if it admits a global uniform hyperbolic structure, i.e.,
where and
are
-invariant subbundles such that there exists
with the property that
is (uniformly) contracted by
and
is (uniformly) contracted by
.
This “uniformity” of Anosov diffeomorphisms was exploited by D. Anosov and Y. Sinai to show the following result:
Theorem 1 Let
be an Anosov diffeomorphism. Then,
is ergodic.
The basic mechanism behind this theorem is the so-called Hopf’s argument, and the smoothness requirement is imposed to ensure that Hopf’s argument works. In particular, it is not known whether Anosov-Sinai theorem holds for
.
In any case, an immediate corollary of Anosov-Sinai theorem is the fact that contains a
-open set of ergodic diffeomorphisms whenever
contains Anosov diffeomorphisms: indeed, this follows from the
–openness of the condition of existence of global uniform hyperbolic structure (see, e.g., Hasselblatt-Katok’s book for more details).
In summary, it is not known that ergodicity is -open among
conservative Anosov diffeomorphisms, but, at least, it is
-open among
conservative Anosov diffeomorphisms. Of course, this scenario motivates the question: given that we don’t know concrete examples of
-open sets of ergodic
-diffeomorphisms, what can be said about the
–genericity (in Baire sense) of ergodicity?
The next theorem by A. Avila, S. Crovisier and A. Wilkinson gives an answer to this question:
Theorem 2 (A. Avila, S. Crovisier and A. Wilkinson) There exists
a residual (i.e.,
-dense) subset such that for any
:
- (ZE) either all Lyapunov exponents
of
-a.e.
vanish,
- (NUA) or
is non-uniformly Anosov in the sense that
has a (global) dominated splitting, i.e., there is a decomposition
into
-invariant subbundles such that
dominates
, that is, there exists
with
for any
,
unitary vectors (“the largest expansion along
is dominated by the weakest contraction in
, but, a priori, neither
is assumed to be contracted nor
is assumed to be expanded”).
- for
-a.e.
, the fibers of
and
of the dominated splitting coincide with the stable and unstable Oseledets subspaces, i.e.,
and
,
and
is ergodic.
Remark 3 The attentive reader will notice that there is no ergodicity claim in item (ZE) and this is not by chance: in fact, the issue of ergodicity in the context of (ZE) is open and it is an interesting problem to understand this question even for particular cases of (ZE) such as “KAM-like examples”.
Remark 4 By definition, a non-uniformly Anosov diffeomorphism is non-uniformly hyperbolic in the sense of Pesin’s theory. In other words, non-uniformly Anosov systems form a intermediate class of dynamical systems between Anosov diffeomorphisms and non-uniformly hyperbolic diffeomorphisms.
Remark 5 In terms of Lyapunov exponents, this theorem says that
-generically there is no “intermediate behavior”: either all Lyapunov exponents are zero (like in KAM examples) or they are all non-zero (and the “Oseledets splitting” is dominated).
Remark 6 For
, this theorem was previously known from the works of R. Mañé and J. Bochi, and, more recently, J. Rodriguez-Hertz showed this theorem for
.
Remark 7 The distinction between the possibilities (ZE) (zero exponents) and (NUA) (non-uniformly Anosov) can be done in terms of the metric entropy
of
. More precisely, we claim that (ZE) occurs if and only if
, and (NUA) occurs if and only if
. Indeed, by Ruelle’s inequality,
. Thus, if all Lyapunov exponents vanish,
, and, if
, then (some) Lyapunov exponents are non-zero. In order to complete the picture, we invoke Pesin’s formula saying that Ruelle’s inequality is an equality in favourable situations: usually Pesin’s formula is stated for
-diffeomorphisms, but W. Sun and X. Tian showed that it is also true in our current context (of
-generic conservative diffeomorphisms) to show that if
then (generically) all Lyapunov exponents must vanish.
After getting some positive result (namely, Theorem 2) for the question of -genericity of ergodicity, it is natural to come back to the question of openness/stability of ergodicity.
Partly motivated by the situation in Anosov-Sinai theorem, we say that ,
, is
–stably ergodic if all
-close to
is ergodic (with respect to
).
By definition and Anosov-Sinai theorem, all Anosov diffeomorphisms are
-stably ergodic. Evidently, one can ask for more general classes of stably ergodic dynamical systems, and, after the works of C. Pugh and M. Shub, K. Burns and A. Wilkinson, and F. Rodriguez-Hertz, J. Rodriguez-Hertz and R. Ures, we know that
–partially hyperbolic diffeomorphisms satisfying certain mild (bunching and essential accessibility) conditions are
-stably ergodic. Here,
is called partially hyperbolic if there is a (global) splitting
into
-invariant subbundles such that the stable direction
is uniformly contracted by
, the unstable direction
is uniformly expanded by
(i.e., contracted by
) and the central direction
is dominated by
and dominates
. In the sequel, the set of
-partially hyperbolic (conservative) diffeomorphisms is denoted by
.
Remark 8 Of course, there is no a priori reason to stop at partially hyperbolic diffeomorphisms: indeed, it makes sense to ask stable ergodicity for conservative diffeomorphisms with dominated splittings and for conservative diffeomorphisms without dominated splittings. In the former case, A. Tahzibi constructed examples of stably ergodic conservative diffeomorphisms with dominated splitting (but not partially hyperbolic), but the general situation of stable ergodicity for diffeomorphisms with dominated splitting is not completely understood. In the latter case, as it was pointed out by S. Crovisier, there is no hope for stable ergodicity: in fact, one can exploit the absence of dominated splittings and a “pasting lemma” by A. Arbieto and myself to (generically) contradict ergodicity by producing periodic orbits possessing some invariant neighborhoods.
As it turns out, for the class of
-partially hyperbolic (conservative) diffeomorphisms, it was conjectured by C. Pugh and M. Shub that there is no need for mild conditions for the validity of stable ergodicity:
Conjecture (Pugh-Shub). For , there exists a
-open
–dense subset of
consisting of
-stably ergodic dynamical systems.
In the direction of Pugh-Shub conjecture, A. Avila, S. Crovisier and A. Wilkinson show the following result:
Theorem 3 (A. Avila, S. Crovisier, A. Wilkinson) For
, the set of ergodic diffeomorphisms in
contains a
-open,
-dense subset of
.
Remark 9 This theorem doesn’t exactly solve Pugh-Shub conjecture because they claim
-density of the set of ergodic diffeomorphisms in
(instead of
-density).
Remark 10 For partially hyperbolic diffeomorphisms
whose central direction
is
-dimensional, this result was previously shown by C. Bonatti, M. Viana, A. Wilkinson and myself, and, for
whose central direction
is
-dimensional, this result was previously shown by F. Rodriguez-Hertz, J. Rodriguez-Hertz, A. Tahzibi and R. Ures.
At this point, as we already mentioned above, Sylvain offered to explain some ideas behind the proof of Theorem 2 while postponing the proof of Theorem 3 for another occasion. In fact, after his talk at LAGA (Univ. Paris 13), Sylvain told me that he intends to sketch the proof of Theorem 3 during a talk next Friday (22 February 2013) at Eliasson-Yoccoz seminar in Jussieu (Univ. Paris 6 and 7). In particular, it is likely that I will write a follow-up to this post (hopefully by the end of February/beginning of March) explaining what I could understand from Sylvain’s talk next Friday.
Anyhow, the next (and last) section of this post contains some highlights on the arguments used in the proof of Theorem 2.
2. Some ideas in the proof of Theorem 2
Let us consider a
-generic conservative diffeomorphism. Recall that, by Oseledets theorem, for
-a.e.
, we have a decomposition
into the stable, central and unstable Oseledets subspaces.
Define
Note that are
-invariant subsets of
such that
The first important ingredient in the proof of Theorem 2 is the following semicontinuity result for due to J. Bochi and M. Viana:
Theorem 4 (Bochi-Viana) Given
, we can find a
-invariant subset
such that
admits a dominated decomposition
where
has dimension
,
has dimension
and
.
In fact, the following corollary of this result makes it clear why we called this a “semicontinuity result”:
Corollary 5 (Bochi-Viana) For
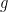
-close to
, the
-measure
of the symmetric difference of
and
is small.
Next, let us notice that the statement of Theorem 2 essentially amounts to say that generically only the “extremal cases”
or occur.
In this direction, we will need the following results of A. Avila and J. Bochi:
Theorem 6 (Avila-Bochi)
is dense and
is ergodic, i.e., there are
and
such that
(mod
).
By putting together the semicontinuity theorem of Bochi-Viana with this theorem of Avila-Bochi, one obtains that:
Corollary 7 If
, then
.
Proof: By Avila-Bochi theorem, there are such that
is a dense subset of
. By Bochi-Viana theorem, there is a dominated splitting
(with
and
) over all
. By definition of dominated splitting, the rates of contraction/expansion along
and
are distinct, so that a (global) dominated decomposition is not compatible with the presence of a positive measure subset where all Lyapunov exponents vanish (or, more generally, are all equal). It follows that
.
At this point, the proof of Theorem 2 is essentially complete if we can show that generically the others (with
) do not show up (i.e., they have zero
-measure).
Before proceeding in this direction, let us make a little detour to briefly explain how one gets ergodicity in the statement of Avila-Bochi theorem. As we told right after the statement of Anosov-Sinai theorem, one usually needs -regularity to obtain ergodicity (at least if one plans to use Hopf-like arguments…). In the context of Avila-Bochi theorem, one can “pretend” that
-generic conservative diffeomorphisms “behave” like
conservative diffeomorphisms as far as the classical ergodicity arguments are concerned. More concretely, by a result of A. Avila, one can
-approximate any
by some
(this is trickier than one might think at first sight: while it is easy to perturb
to improve its smoothness [say by convolution], but it is not so simple to regularize
keeping the conservativeness condition; from the point of view of PDEs, this amounts to solve the Jacobian equation
where
is
…), and one can use some “semicontinuity arguments” (like Bochi-Viana theorem…) to claim that
behaves like a
-generic
.
Anyhow, let us “pretend” that and let us consider
. By some results of A. Katok (strongly based on Pesin’s theory), it is known that we can “approach”
by horseshoes, that is, there are periodic points
,
, such that
where . Here:
and
are the usual stable and unstable manifolds of the (hyperbolic) periodic point
;
and
are the stable and unstable manifolds of
provided by Pesin’s theory; finally,
means that
and
meet transversely.
The sets work as a sort of “homoclinic class in the sense of Pesin”, and, as it was shown by F. Rodriguez-Hertz, J. Rodriguez-Hertz, A. Tahzibi and R. Ures, they are good enough to play with a (generalized) Hopf argument:
Theorem 8 (Rodriguez-Hertz, Rodriguez-Hertz, Tahzibi, Ures) For any hyperbolic periodic point
,
is ergodic (if
is
).
So, the proof of Avila-Bochi theorem (that is ergodic) will be complete if we can “connect together” the several “homoclinic classes”
in order to obtain a single ergodic piece. Here, one can use the connecting lemma for pseudo-orbits of C. Bonatti and S. Crovisier saying that, for a
-generic
, any pair of hyperbolic periodic points
and
are connected in the sense that either
or
.
Coming back to the main discussion (i.e., the completion of the proof of Theorem 2), let us explain how to get rid of the “other” ‘s, that is, let us show that generically one has
when
.
The basic idea to “destroy” is to delete some central (zero) Lyapunov exponents. More concretely, we consider a subset
such that
is very small and
has dominated splitting
where
and
. By definition, the subbundle
contains all zero Lyapunov exponents, so that we will destroy
(or at least
, a large piece of
) if we can convert some exponents in
into non-zero Lyapunov exponents. In this direction, Avila, Crovisier and Wilkinson prove the following theorem:
Theorem 9 Let
and consider
an open set. Denote by
the maximal invariant set of
, i.e.,
and suppose that
has a dominated splitting
such that
for
-a.e.
. Then, for any
, there exists
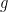
-close to
such that
In other words, this theorem says that, if the sum of Lyapunov exponents in is non-positive, then we can perturb the dynamics to get that the sum of Lyapunov exponents in
is negative except for a set of small
-measure.
Remark 11 For the case
,
thisa similar result was proved by M. Shub and A. Wilkinson (for a important class of partially hyperbolic diffeomorphisms), and A. Baraviera and C. Bonatti (in general).
Using Theorem 9, one can destroy with
by induction: starting with
with
and
as large as possible, one can apply Theorem 9 to convert
into a subset of
or another
with
and
.
Completing this post, let us say a few words about the proof of Theorem 9. We take a small ball of radius
. Consider
a diffeomorphism such that
is the identity outside
, and
is a small rotation of
towards
say (for a mental picture you can think of
as the
-axis,
as the
-axis,
as the
-axis in
and
as a small rotation in the
-plane) in the ball
with the same center of
and radius
.
If we consider the action of the derivative of on
along the orbits of points starting at
, we will see that
is tilted towards
at the first step, and, in the next steps, the component of
on
gets contracted while the component of
on
stays about the same size.
In summary, this perturbation permits to the (sum of) Lyapunov exponents in slightly more negative along the orbits passing through the ball
. Of course, there is a trade in this perturbation: since
is an interpolation between a small rotation and the identity, it turns out that the effect on Lyapunov exponents of orbits passing through
is the opposite of the expected one. In the case
, this is not a big problem: this “boundary effect” can be controlled by arguing that most orbits (with respect to the volume
) will not see
(possibly after adjusting the ratio between the radius of
and
to get closer to
…). However, since we don’t know the set
in advance, it could be that the a large part of orbits in the maximal invariant set
will feel the boundary effect. At this point, Avila-Crovisier-Wilkinson borrow the following idea of J. Bochi: instead of performing a small rotation in the ball
, one can iterate this produce to kill the boundary effect as follows: starting with
, one iterates by
and one lands in a ball
. Now, one divides
into a certain number of small balls and one performs another round of small independent rotations on each of these balls, and one continues by induction (i.e., subdividing the iterate of each ball and performing independent rotations). Of course, we are hidden lots of details (for instance, how to choose the parameters for the division of balls and for the rotations), but we will not comment more on this point (leaving the curious reader to consult Subsection 2.3 of Bochi’s paper for a more precise description of this idea).
Update (March 25, 2013): As it was pointed out to me by Artur (Avila), the previous version of Remark 11 was not accurate: in fact, Shub-Wilkinson and Bonatti-Baraviera were able to change just the sign of the *average* of the Jacobian over the whole manifold
over the whole manifold 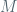 , while Theorem 9 allows to change the sign of
, while Theorem 9 allows to change the sign of  in a subset almost full measure of
in a subset almost full measure of  .
.
By: matheuscmss on March 25, 2013
at 1:18 pm